字典树
简介
字典树,又称单词查找树、前缀树,是一种树形结构,属于哈希树的变种,在统计、排序、保存大量字符串时具有很小的时间复杂度,常用于搜索引擎系统用于文本词频的统计,其优点在于利用字符串的公共前缀来减少查询时间,最大限度减少没有意义的字符串比较,查找效率比哈希树高。 比如我有"a","apple","appeal","bee","beef","cat"这七个单词,就能够组成下面图示的字典树,如果我们需要获得"apple"这个单词的信息,按顺序访问对应的结点即可 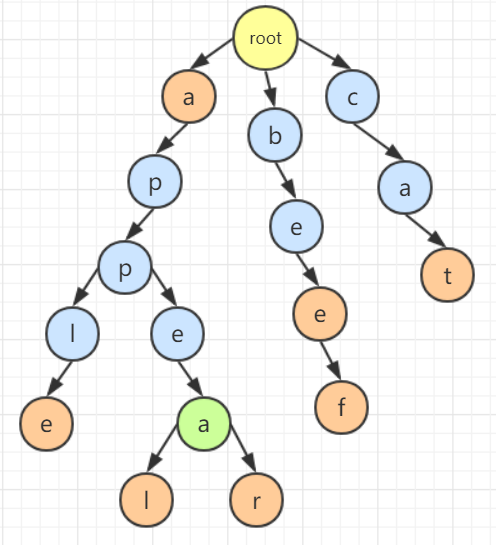 ### 字典树的性质 1. 根节点不包含字符,除根节点外每个结点有且仅有有一个字符 2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串 3. 每个节点的所有子节点包含字符各不相同
### 字典树的性质 1. 根节点不包含字符,除根节点外每个结点有且仅有有一个字符 2. 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串 3. 每个节点的所有子节点包含字符各不相同
字典树的应用
- 字典:字符串集合对应一定的信息
- 计算热词:统计字符串在集合中出现的元素
- 串的快速检索:给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,按最早出现的顺序写出所有不在熟词表中的生词,我们可以把熟词建成字典树,然后读入文章进行比较
- 串排序:给出N个互不相同的仅由一个单词构成的英文名,让他们按字典序从小到大输出,采用数组的方式创建字典树,这棵树的每个节点的儿子很显然按照其字母大小排序,对这棵树进行先序遍历即可
- 最长公共前缀:对所有串建立字典树,对两个串的最长公共前缀长度就是他们所在节点的公共祖先个数 ## 具体实现 ### 顺序储存结构 #### 节点结构体定义 我们先开辟一个足够大的数组,这里我们使用静态链表的思想,用游标表示节点的后继,我们在结构体中开辟一个数组来描述节点的后继,这里可以确定其长度为26,然后再定义一个bool类型,判定是否为单词的结尾 #### 插入操作
1
2
3
4
5# define MAXSIZE 26
struct node{
bool flag;
int next[MAXSIZE];
}trie[100001]#### 查询操作1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20void Insert(char *str,int *space)
{
\*space表示第一个空闲节点的下标,str为插入的字符串,idx为挖掘层数,order将字符转化为在字母表中的顺序
*\
int order;
int idx; //从第一层开始向下挖掘
for(int i=0;i<strlen(str);++i)
{
order = str[i]-'a';
if(trie[idx].next[order] == 0)//idx没有该字符的子节点
{
trie[idx].next[order] = space++;//启用第space号节点,copy新节点的编号
idx = trie[idx].next[order];//idx节点对应的后继为space
trie[idx].flag = false;//标记新节点不是单词的结尾
}
else
idx = trie[idx].next[order];//前缀存在继续挖掘
}
trie[idx].flag = true;//表示单词结尾
}### 链式储存结构 #### 节点结构体定义1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19bool Find(char *str)
{
int order;
int idx=1;
for(int i=0;i<strlen(str);++i)
{
order = str[i]-'a';
if(trie[idx].next[order]==0)//若字母失配,匹配结束
{
return false;
}
idx = trie[idx].next[order];//存在对应字母,匹配继续
}
if (trie[idx].flag == false)//若成功匹配,但不为单词结尾
return false;
else
return true;
}#### 插入操作1
2
3
4
5typedef struct Node
{
Node *next[26];
bool flag;
}Node, *Trie;#### 查询操作1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void buildTrie(Trie root,char *word)
{
Trie pre = root;
Trie ptr;
int order;
for(int i=0;i<strlen(word);++i)//字母序对应后继不存在
{
order = word[i]-'a';
if(pre->next[order] == NULL)
{
ptr = (Node *)malloc(sizeof(Node));//初始化新节点
for(int j=0;j<26;++j)
ptr->next[j]==NULL;
ptr->fail = NULL;
ptr->flag = false;
pre->next[order] = ptr;//插入新节点
}
pre = ptr->next[order];//用新节点作为下一次循环的根节点
}
pre->flag = true;//修改flag表示为单词结尾
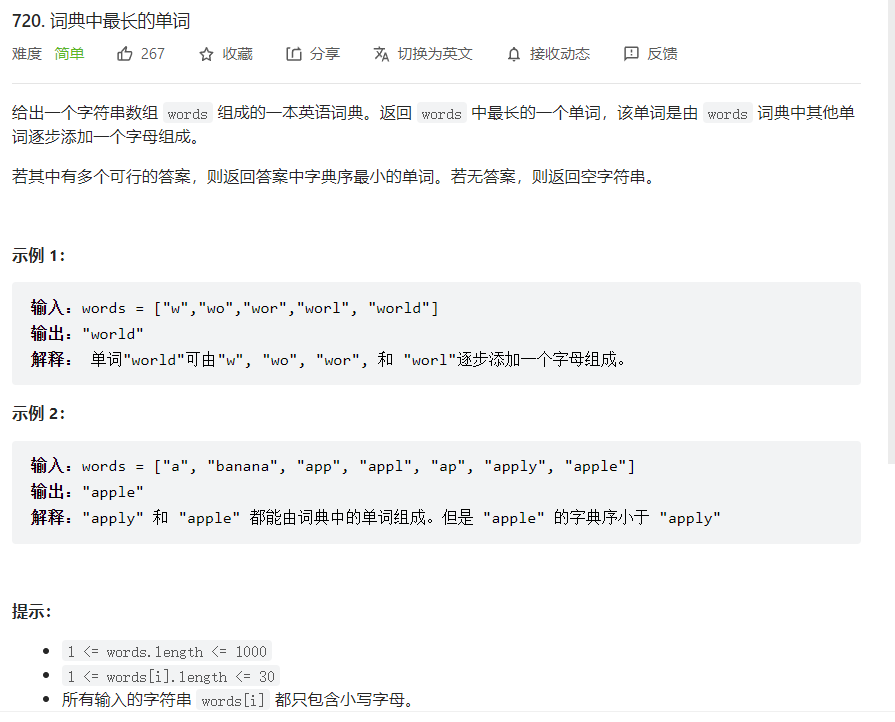
}### 例题详解 #### leetcode 720(词典中最长的单词) 题目描述如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28bool Find(char * str)
{
int order;
Trie pre= root
Trie ptr;
int length = strlen(str);
if(!length)
{
return 0;
}
for(int i=0;i<length;++i)
{
order = str[i]-'a';
if(pre->next[order] == NULL && pre!=root)
{
return false;
}
pre = pre->next[order];
}
if(pre->flag==false)
{
return false;
}
else
{
return true;
}
} ##### 思路和算法
##### 思路和算法
由于符合要求的单词的每个前缀都是符合要求的单词,因此可以使用字典树存储所有符合要求的单词。 创建字典树,遍历数组 words,并将每个单词插入字典树。当所有的单词都插入字典树之后,将答案初始化为空字符串,再次遍历数组 words,判断每个单词是否是符合要求的单词,并更新答案。如果一个单词是符合要求的单词,则比较当前单词与答案,如果当前单词的长度大于答案的长度,或者当前单词的长度等于答案的长度且当前单词的字典序小于答案的字典序,则将答案更新为当前单词。
代码
1 | #define MAX_STR_LEN 32 |