图的存储结构

前言

最近笔者在准备数据结构考试，故复习了些课本知识，发下自己对与图的存储结构还有诸多遗漏，故特意整理了些图的存储结构笔记，图的存储结构相对来说比较复杂，望大家复习时不要遗漏 ## 邻接矩阵 该储存方式是由两个数组来表示图1，一个一维数组储存图中顶点信息，一个二维数组(即为邻接矩阵)储存图中的边或弧的信息 具体实例： 无向图 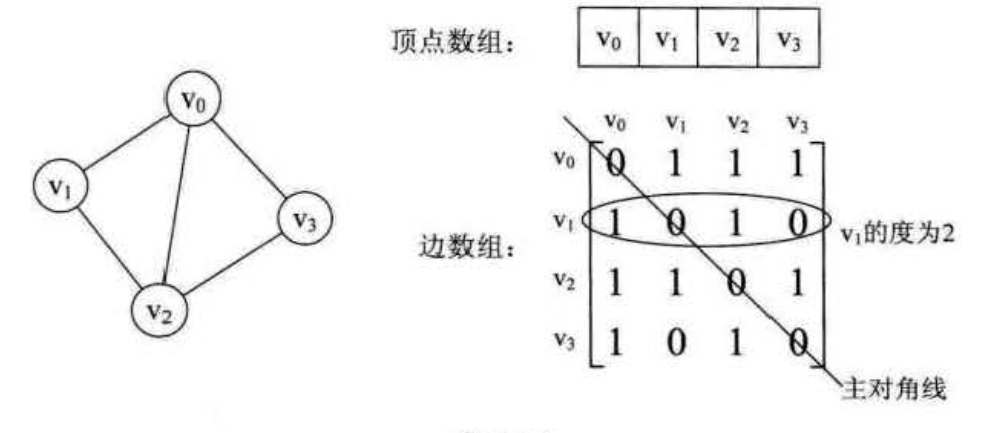可以很容易看出无向图的边数组是一个对称矩阵。 有了该矩阵后，我们可以： 1. 判定任意两顶点是否有边无边 2. 确定某个顶点的度。就是该顶点的行(列)的元素之和。 3. 求某顶点的所有邻接点就是把矩阵该行元素全部扫描一遍，为一的就是邻接点 有向图 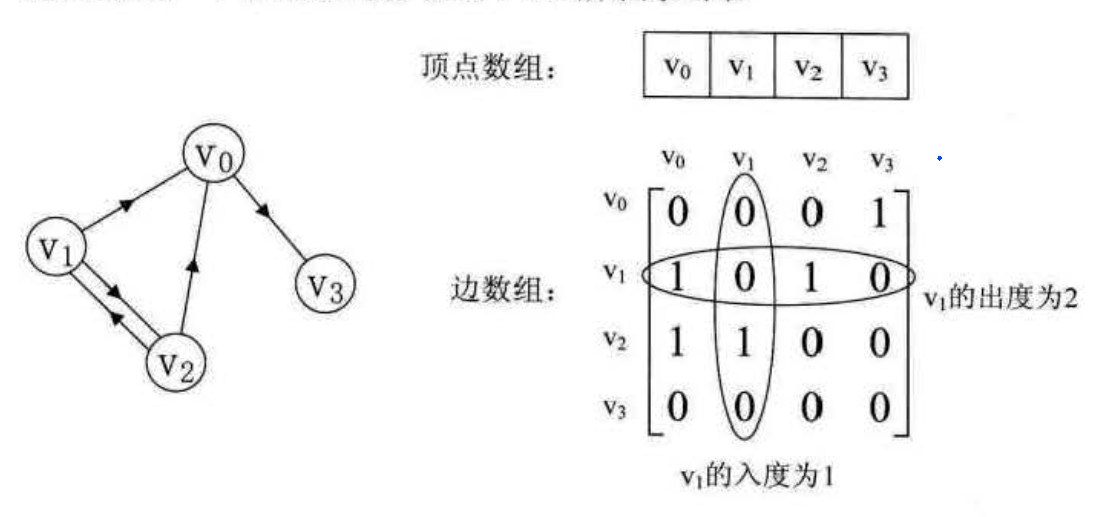有向图讲究的入度和出度，入度对应列，出度对应行 带权值的有向图 就把有向图中为0的地方数组改为无穷，其余地方的值为该边上的权值即可 缺点 对于边数相对顶点较少的图，这种结构对储存空间造成极大浪费 ## 邻接表 顶点用一个一维数组储存，便于读取顶点信息，其次还要储存一个指向第一个邻接点的指针，便于查找该顶点的边信息 顶点所有邻接点构成一个线性表，用单链表储存，无向图称为顶点的边表，有向图称为顶点作为弧尾的出边表 具体实例如下： 无向图 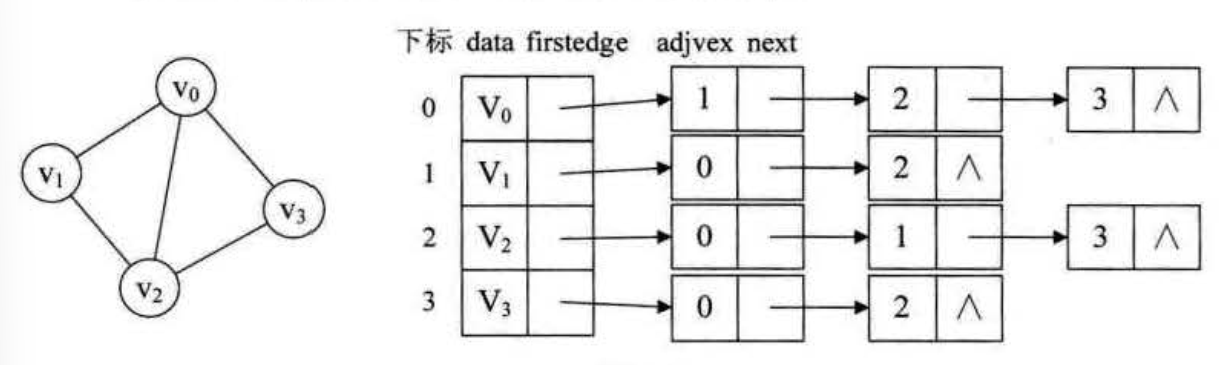每个节点有data，firstedge两个域表示，data储存顶点信息，firstedge指针域，指向边表的第一个节点，边表节点由adjvex和next两个域组成，adjvex储存邻接点在顶点表的下标，next指向边表下一个节点的指针

有向图 有向图的邻接表结构是类似的，但由于它有方向，我们以顶点为弧尾储存边表，很容易可以得到每个顶点的出度，如果要得到每个顶点的入度，可构建一个逆邻接表 示意图如下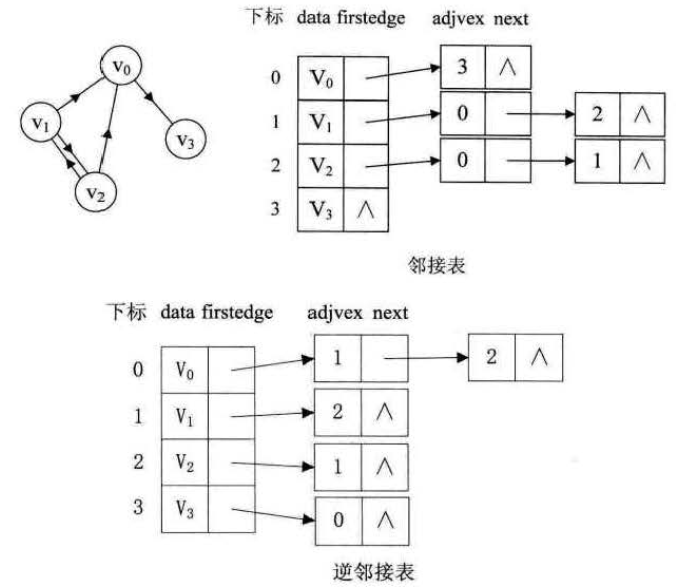

带权值的有向图 只需在边表节点定义中加一个weight的数据域，储存权值信息即可 缺点 对于有向图来说，邻接表不能同时了解入度出度问题 ## 十字链表 顶点表节点包括data，firstin，firstout，分别表示数据，入边表头指针，出边表头指针 边表节点结构包括tailvex，headvex，headlink，taillink，分别代表弧起点，弧终点，入边表指针域，指向终点相同的下一条边，出边表指针域，指向起点相同的下一条边，如果是网，还可以增加一个weight域来储存权值 示意图如下：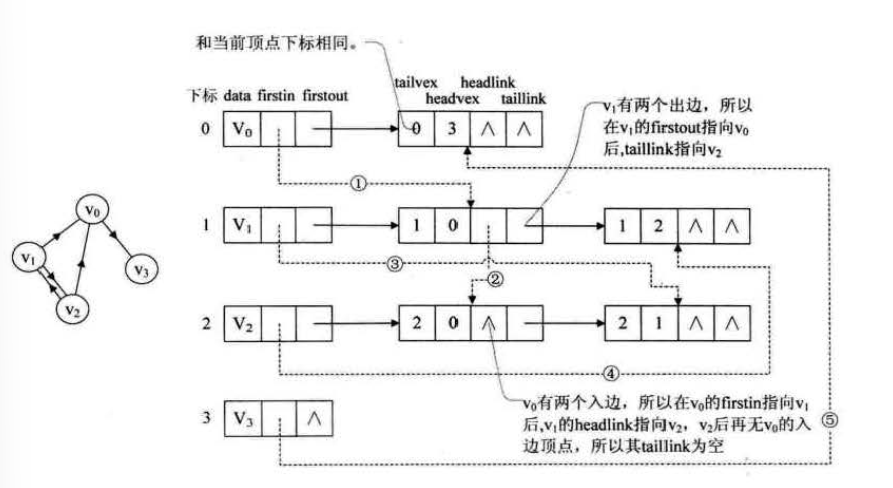

优缺点 好处在于容易找到顶点的入出度，但其结构复杂点，但创建时间复杂度和邻接表相同，所以在有向图的应用中，它是一个非常好的模型

邻接多重表

只需要在邻接表基础上，对边表节点进行一些改造，重新定义的边表结构如下：ivex，ilink，jvex，jlink，分别为边对应的两个顶点下标，指向依附ivex的下一条边，指向依附jvex的下一条边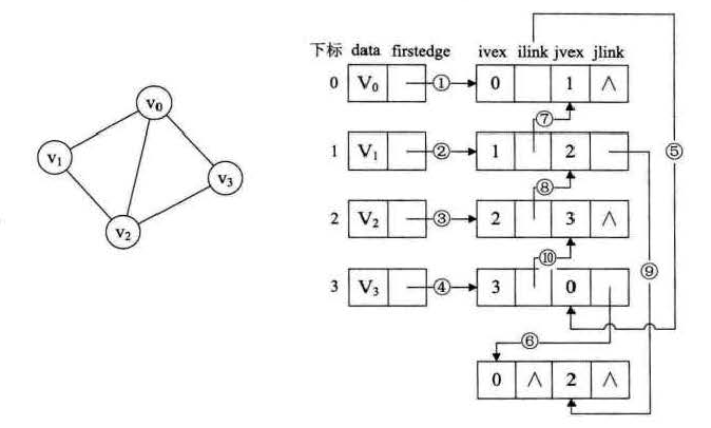

与邻接表的区别 一条边在邻接表中要用两个节点表示，而在邻接多重表中只有一个节点，这样对边的操作更方便

边集数组

有两个一维数组构成，一个储存顶点信息，一个储存边的信息，边数组数据元素由边起点下标begin，终点下标end，权值weight组成，它不适合对顶点操作，更适合对边的操作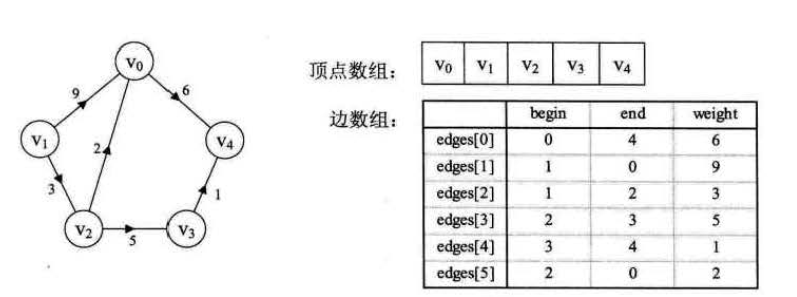

参考资料

程杰《大话数据结构》