次优查找树

前言

关于静态查找表中对特定关键字进行顺序查找，折半查找或者分块查找，都是在查找表中各关键词被查找概率相同的前提下进行的，然而在查找表中各关键字查找概率不同的情况下，折半查找的效果其实是不好的。在查找成功的情况下，描述查找过程的判定树其带权路径长度之和（用PH表示）最小时，查找性能最优，称该二叉树为静态最优查找树 其中: PH = 所有节点所在的层次数*每个节点对应的概率值 由于构造最优查找树花费的时间代价较高，而且有一种构造方式创建的判定树的查找性能同最优查找树只差1%-2%，称这种极度接近于最优查找树的二叉树为次优查找树

创建方法

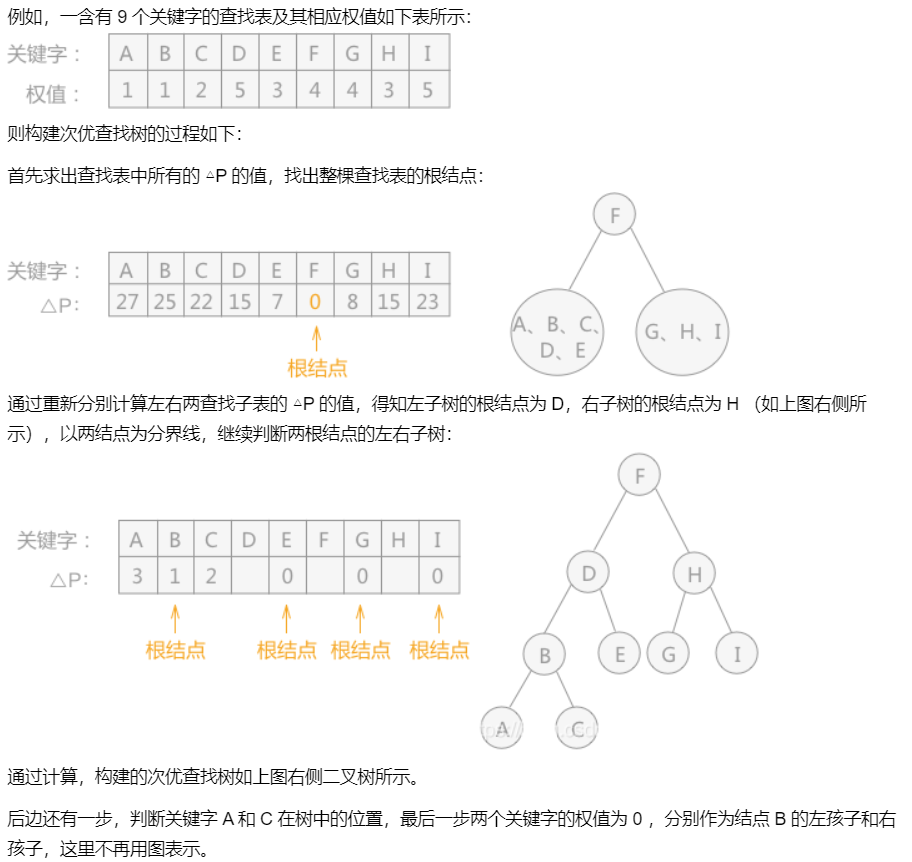
首先取出标准每个关键字及其对应的权值，采用如下公式计算出每个关键字对应的一个值： \(\triangle P_i= \left|\sum\limits_{j=i+1}^hw_j-\sum\limits_{j=1}^{i-1}w_j\right|\) 其中 wj 表示每个关键字的权值（被查找到的概率），h 表示关键字的个数。 表中有多少关键字，就会有多少个 △Pi ，取其中最小的做为次优查找树的根结点，然后将表中关键字从第 i 个关键字的位置分成两部分，分别作为该根结点的左子树和右子树。同理，左子树和右子树也这么处理，直到最后构成次优查找树完成。 ## 代码实现

typedef int KeyType;　　// 定义关键字类型
typedef struct
{
    KeyType key;
}ElemType;　　// 定义元素类型


typedef struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

// 定义变量
int i;
int min;
int dw;

//创建次优查找树，R数组为查找表，sw数组为存储的各关键字的概率（权值），low和high表示的sw数组中的权值的范围
void SecondOptimal(BiTree T, ElemType R[], float sw[], int low, int high)
{
    // 由有序表R[low...high]及其累计权值表sw（其中sw[0]==0）递归构造次优查找树
    i = low;
    min = abs(sw[high] - sw[low]);
    dw = sw[high] + sw[low - 1];
    // 选择最小的△Pi值
    for (int j = low+1; j <=high; j++)
　　{
        if (abs(dw - sw[j] - sw[j-1]) < min)
　　　　 {
            i = j;
            min = abs(dw - sw[j] - sw[j - 1]);
        }
    }
   
    T = (BiTree)malloc(sizeof(BiTNode));
    T->data = R[i];　　// 生成结点（第一次生成根）
    if (i == low) 
　　 　　T->lchild = NULL;　　// 左子树空
    else SecondOptimal(T->lchild, R, sw, low, i - 1);　　// 构造左子树
    if (i == high) 
　　 　　T->rchild = NULL;　　//右子树空
    else 
　　　　SecondOptimal(T->rchild, R, sw, i + 1, high);　　//构造右子树   
}

## 具体实例 注意 在建立次优查找树时，由于只根据各关键字的P的值进行构建，没有考虑单个关键字的相应权值大小，有时会出现根节点权值比孩子节点权值还小，这时需要适当调整二者位置

总结

由于使用次优查找树和最优查找树的性能差距很小，构造次优查找树的算法的时间复杂度为 O(nlogn)，因此可以使用次优查找树表示概率不等的查找表对应的静态查找表（又称为静态树表）。 ## 参考资料 如是说的博客