夏至的个人博客

最小生成树(Prim算法，Kruskcal算法)

发表于 更新于 分类于
本文字数： 3.1k 阅读时长 ≈ 3 分钟

前言

最小生成树由一个经典的架电线的问题引出：在n个村庄间架电线，现在已经知道各村庄的相对距离，如果你是工程师，请问如何设计能使得总造价最小

解决思路

首先可以分析得到这显然是一个带权值的图，即网结构，我们的目标可以抽象为用n-1条边把一个连通图连接起来，并使得权值最小，这就是我们常说的最小生成树问题，最经典的两种算法是：prim算法和kruskcal算法，下文将一一介绍 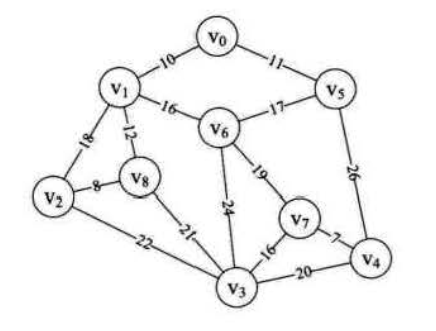最小生成树.png

prim算法

算法思路

该算法的核心是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树，因为这里涉及到顶点与顶点的带权值边信息，所以我们考虑使用邻接矩阵作为储存结构来实现，如果不清楚邻接矩阵，请戳图的存储结构 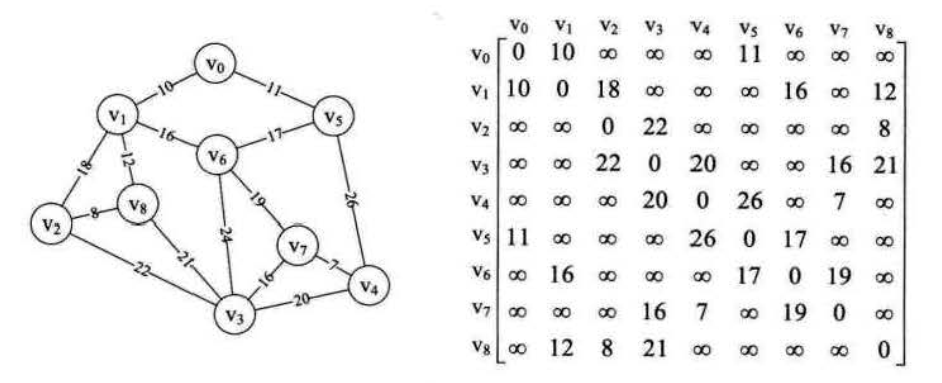最小生成树-邻接矩阵.png 这样一来，我们已经有了一个以邻接矩阵为存储结构的网，我们下面该如何求最小生成树呢?其实很简单，我们在prim算法的开头就说过，该算法的核心是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树，我们就先去一个顶点来研究，默认为v0，然后把v0在邻接矩阵中所对应的那一行信息取出(用一个lowcost数组保存)，目的是研究以v0为起点，与其相连最近的顶点。然后我们遍历一遍lowcost数组，找到其数组中除了本节点(即v0-0)外的最小值，记录下它的值与下标-此时的low cost数组中lowcost[0]=0,表示该位置对应节点已加入最小生成树，连接该下标所对应的顶点与v0，构成第一条电线，在这里对应的是v1，在找到v1后，我们把lowcost该位置的值设为0，表示该节点已经被纳入了最小生成树，然后我们再去取出v1在邻接矩阵中对应行的信息，将其与lowcost数组的对应值相比较，若更小则修改lowcost值，该操作的目的是找到v0,v1这两行连接信息中的最小值来形成第二根电线，接下来的操作也和上面的操作类似了，直到所有节点都添加到最小生成树中，lowcost数组全部置为0，表明最小生成树生成完毕。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/* Prim算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph G){
	int min, i, j, k;
	int adjvex[MAXVEX];	//保存相关顶点下标
	int lowcost[MAXVEX];	//保存相关顶点间边的权值
	lowcast[0] = 0;	//初始化第一个权值为0，即v0加入生成树，lowcost的值为0，在这里就是此下标的顶点已经加入生成树
	adjvex[0] = 0;	//初始化第一个顶点下标为0
	for(i = 1;i<G.numVertexes;i++){	//循环除下标为0外的全部顶点
		lowcost[i] = G.arc[0][i];		//将v0顶点与之有边的权值存入数组
		adjvex[i] = 0;	//初始化都为v0的下标
	}
	for(i=1;i<G.numVertexes;i++){
		min = INFINITY;	//初始化最小权值为无穷大，通常设置为很大的数字
		j = 1;
		k = 0;
		while(j<G.numVertexes){		//循环全部顶点
			if(lowcost[j] != 0 && lowcost[j] < min){	//如果权值不为0且权值小于min
				min = lowcost[j];		//让当前权值成为最小值
				k = j;		//将当前最小值的下标存入k
			}
			j++;
		}
		printf("(%d,%d)",adjvex[k],k);	//打印当前顶点边中权值最小边
		lowcost[k] = 0;	//将当前顶点的权值设置为0，表示此顶点已经完成任务
		for(j=1;j<G.numVertexes;j++){	//循环所有顶点
			if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j]){	//若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值
				lowcost[j] = G.arc[k][j];		//将较小权值存入lowcost
				adjvex[j] = k;	//将下标为k的顶点存入adjvex
			}
		}
	}
}

由算法代码中的循环嵌套可知该算法时间复杂度为O(\(n^2\))

Kruskal算法

算法思路

与prim算法不同的是，prim算法以顶点为目标构造最小生成树，而Kruskal算法直接以边的目标去构造，每次找最小权值的边来构成最小生成树，但是，因为我们在构建时是以边为目标，必须要考虑边的闭环问题,因为可能出现要铺设九个村庄的电线，但在三个村庄间就出现了闭环，导致存在环与环之间无法互联的现象，这个问题出现的原因是因为我们如果只研究边的权值大小，会忽略顶点与顶点互联的要求，因为是对边的权值大小直接进行研究，这里我们最好使用边集数组作为存储结构，不会请戳图的存储结构 这里我们需要先将边集数组按照权值从小到大进行下转换。 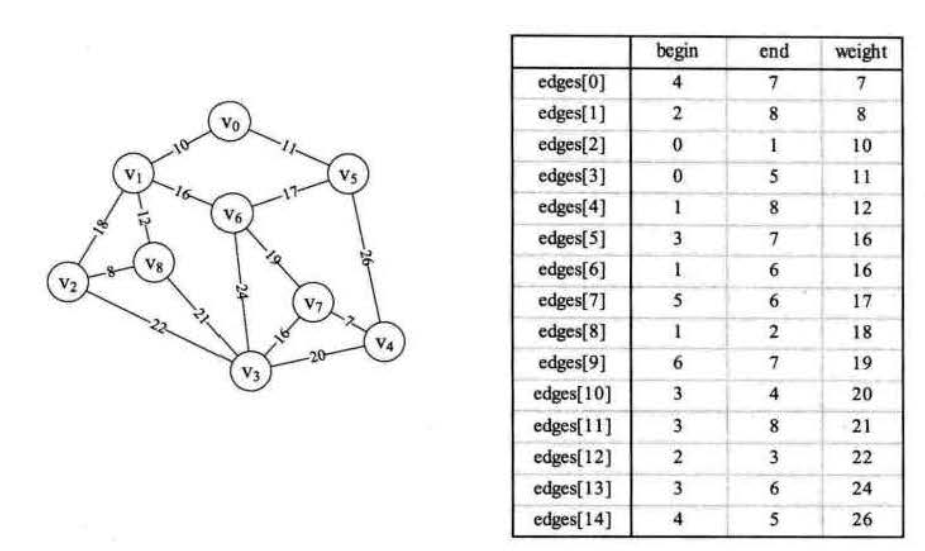最小生成树-边集数组.png 我们对边集数组做循环遍历，每当你要添加一个边时，必须先调用一个find函数来判断该边对应的起点和终点在当前的最小生成树数组中是否会构成闭环，如果会，则舍弃接着往后，不会则添加，这个find函数借助了一个parent数组，我们将其初始化为0，每当添加一条边，就将对应起点的parent数组值修改为该边的终点，然后find函数判断连线顶点的尾部下标，如果和原来尾部对应下标经find函数处理返回值一致，说明形成了环，舍弃该边

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/* kruskal算法生成最小生成树 */
void MiniSpanTree(MGraph G){	//生成最小生成树
	int i, n, m;
	Edge edges[MAXEDGE];	//定义边集数组
	int parent[MAXVEX];	//定义一数组用来判断边与边是否形成环路
	/* 此处省略将邻接矩阵G转化为边集数组edges并按权由小到大排序的代码 */
	for(i = 0;i<G.numVertexes;i++)
		parent[i] = 0;	//初始化数组值为0
	for(i = 0;i<G.numEdges;i++){	//循环每一条边
		n = Find(parent, edges[i].begin);
		m = Find(parent, edges[i].end);
		if(n != m){		//假如n与m不等，说明此边没有与现有生成树形成环路
			parent[n] = m;	//将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中
			printf("(%d,%d) %d", edges[i].begin, edges[i].end, edges[i].weight);
		}
	}
}

int Find(int* parent, int f){	//查找连线顶点的尾部下标
	while(parent[f] > 0)
		f = parent[f];
	return f;
}

该算法的时间复杂度为O(eloge),e为边数

总结

对比两个算法来说，Kruskcal算法主要针对边来展开，边数少的时候效率会非常高，对于稀疏图有很大的优势，而Prim算法对于稠密图，边上非常多的情况会更好一些(个人认为是因为边数少是Kruskcal出现闭环的可能性小，在这种情况下，其效率会比Prim算法高很多，然后边数多了以后，出现闭环的可能性大大增加，导致其效率反而不如Prim算法了)

参考资料

《大话数据结构》程杰