前言

在学习邻接矩阵时，我们会发现一个有意思的现象，有时100*100的矩阵中只储存了10个数据，我们把这种矩阵称为稀疏矩阵，其适用于一个阶数较大的矩阵中的非零元素个数相对于矩阵元素的总个数很小，如果这种稀疏矩阵用邻接矩阵来储存，这是浪费了很多空间的，那么我们应当如何在保留其矩阵信息的前提下，用一个好的结构来节省空间的开支呢？ # 三元组 ## 定义三元组是一种稀疏矩阵的压缩储存方式，其储存策略是只储存非零元素，它的储存方案是： 1. 储存非零元素 2. 同时储存该非零元素所对应的行下标和列下标 3. 稀疏矩阵中的每一个非零元素由一个三元组元素唯一确定，稀疏矩阵的所有非零元素构成三元组线性表，三元组的i为行下标，j为列下标，data域是对应的元素值 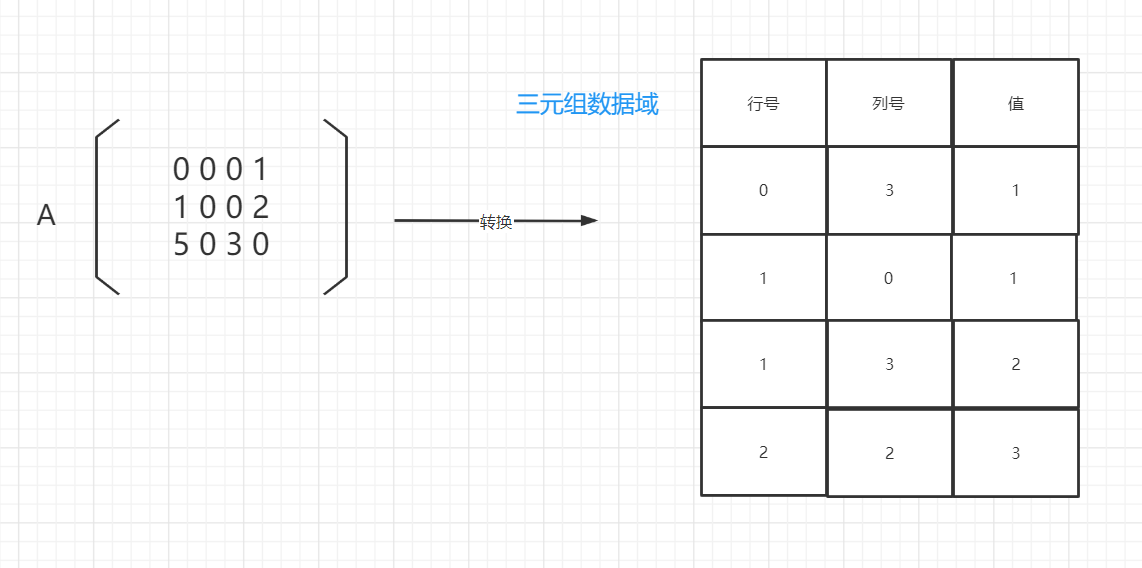## 储存结构下面直接上代码，注释写的比较清楚

#define MaxSize 100

//定义三元组线性表中的数据元素存储结构
typedef struct
{
    int row;        //行号
    int col;        //列号
    ElemType d;     //元素值，ElemType为数据元素类型

} TupNode; //三元组定义


//定义三元组线性表存储结构
typedef struct
{
    int rows;                   //行数值
    int cols;                   //列数值
    int nums;                   //非零元素个数
    TupNode data[MaxSize];      //data数据域

} TSMatrix; //三元组顺序表定义

## 基本运算 ### 扫描二维矩阵，创建三元组

//以行序方式扫描二维矩阵A，将其非零的元素加入到三元组t
//以3行4列的稀疏矩阵为例
void CreatMat(TSMatrix *t, int arr[3][4])
{
    int i;
    int j;
    t->rows = 3;
    t->cols = 4;
    t->nums = 0;

    //扫描矩阵中的非零元素
    for(i = 0; i < 3; i++)
    {
        for(j = 0; j < 4; j++)
        {
            //只存非零值，以三元组方式
            if(arr[i][j] != 0)
            {
                t->data[t->nums].row = i;
                t->data[t->nums].col = j;
                t->data[t->nums].d = arr[i][j];
                t->nums++;
            }
        }
    }
}

## 将三元组指定位置元素值赋给对象

//将三元组线性表中指定位置的元素值赋值给变量x
void arr_Assign(TSMatrix t , int *data , int i , int j)
{
    int k = 0;
    //i和j是否合法
    if(i >= t.rows || j >= t.cols)
    {
        return;
    }

    //找到指定元素的行下标
    while(k < t.nums && i > t.data[k].row)
    {
        k++;
    }

    //当找到指定元素的行下标后，再找到指定元素的列下标
    while (k < t.nums && i == t.data[k].row && j > t.data[k].col)
    {
        k++;
    }
    //如果指定元素的行和列都相等，说明找到了
    if(t.data[k].row == i && t.data[k].col)
    {
        *data = t.data[k].d;
    }
    else
    {
        //说明没找到
        *data = 0;
    }
}

## 对三元组元素赋值

//修改三元组元素中的值：执行A[i][j]=x
void arr_Value(TSMatrix *t , int data , int i , int j)
{
    int k = 0;
    int k1;
    //指定的行和列是否合法
    if(i >= t->rows || j >= t->cols)
    {
        return;
    }
    //先查找行
    while(k < t->nums && i > t->data[k].row)
    {
        k++;
    }

    //查找列
    while(k < t->nums && i == t->data[k].row && j > t->data[k].col)
    {
        k++;
    }

    //当找到指定位置时直接修改
    if(i == t->data[k].row && j == t->data[k].col)
    {
        t->data[k].d = data;
    }
    else
    {
        //如果指定位置不存在，则说明该元素值为0，此时插入
        for(k1 = t->nums; k1 >= k; k1--)
        {
            t->data[k1+1].col = t->data[k1].col;
            t->data[k1+1].row = t->data[k1].row;
            t->data[k1+1].d = t->data[k1].d;
        }
        //插入数据
        t->data[k].row = i;
        t->data[k].col = j;
        t->data[k].d = data;
        t->nums++;
    }
}

# 参考资料 songly_的博客

夏至的个人博客

稀疏矩阵的三元组表示

前言