引言
本章与信号与系统知识有较多重复,仅记录部分重要的概念
信号分类
时间-幅度 连续 离散 连续 模拟 抽样 离散 量化 数字
离散时间信号-序列
常见序列
单位取样序列\[\delta(n)=\begin{cases} 1,n=0\\ 0,n\ne0 \end{cases},\delta(n-n_0)=\begin{cases} 1,n=n_0\\ 0,n\ne n_0 \end{cases}\\ x(n)\delta(n)=x(0)\qquad x(n)\delta(n-n_0)=x(n_0)\\x(n)*\delta(n-n_0)=x(n-n_0)\qquad x(t)\delta(t)=x(0)\delta(t)\]
单位阶跃序列\[u(n)=\begin{cases} 1,n\ge0\\ 0,n<0 \end{cases},\delta(n)=u(n)-u(n-1)\\ u(n)=\sum_{k=\infty}^n\delta(k)\quad u(n)=\sum_{k=0}^\infty\delta(n-k)\]
矩形序列\[R_N(n)=\begin{cases} 1,0\le n \le N-1\\ 0,others \end{cases},R_N(n)=u(n)-u(n-N)\]
复指数序列和正弦序列\[x(n)=e^{(\sigma+jw)n}=e^{\sigma n}cos(wn)+je^{\sigma n}sin(wn),w-数字域频率\\ 比较:x_a(t)=Asin(\Omega t+\phi)=Asin(2\pi ft+\phi)\]其中:\(\Omega=2\pi f\)模拟域频率,\(w=\Omega T(采样周期)\)
当\(w=0\)时,\(cos(wn)\)变化最慢,当\(w=\pi\)时,\(cos(wn)\)变化最快,在主值空间\([-\pi,\pi]or[0,2\pi]\)上,把\(w=0\)附近称为数字低频,\(w=\pi\)称为数字高频。这一特点与模拟正弦信号完全不同,后者\(\Omega\)越大,变化越快,因为其连续取值
离散时间系统
FIR系统和IIR系统
FIR:有限冲激响应,IIR:无限冲激响应 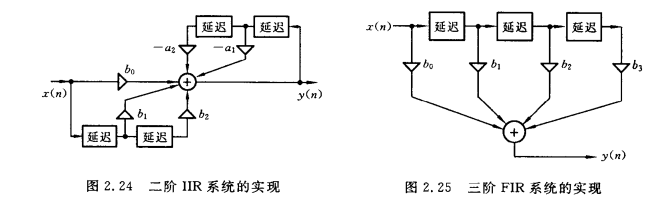
离散时间系统的性质
在判断离散时间系统性质时,一般用到的都是和信号与系统中已经学到的性质,如线性性,稳定性,因果性这些,主要用到的是因果性,稳定性。因果性和稳定性的判断一般可借助系统函数进行判断,系统函数收敛域包含单位圆即稳定,收敛域到无穷即为因果,在一般判断中,用二者即可,在有些习题中可能不给出时域信号是否是右边信号,只给出\(H(z)\),其判断思路可以参考下面这道例题

在这道例题中,没给出时域信号是否为右边信号,但根据其在无穷远处仍存在,且极点在单位圆外,可判断其为因果不稳定
离散时间信号和系统的频域表示
连续信号的FT
重要性质1:当\(x(n)\)为实序列时,\(X(e^{jw})\)的幅值\(|X(e^{jw})|\)在区间\(0\le w\le2\pi\)内是偶对称函数,相位 \(arg[X(e^{jw})]\) 是奇对称函数
离散时间信号的FT的性质
序列的FT的对称性
\(x_e(n)=x_e^*(-n)\) 共轭对称序列
\(x_o(n)=-x_o^*(-n)\) 共轭反对称序列
\(x_e(e^{jw})=x_e^*(e^{-jw})\) 共轭对称函数
\(x_o(e^{jw})=-x_o^*(e^{-jw})\) 共轭反对称函数
这表明\(x_e(n)\)的实部和\(x_o(n)\)的虚部为偶序列,\(x_e(n)\)的虚部和\(x_o(n)\)的实部为奇序列,进一步推导可以得到以下序列分解公式\[x_e(n)=\frac{1}{2}[x(n)+x^*(-n)] \qquad x_o(n)=\frac{1}{2}[x(n)-x^*(-n)]\\X_e(e^{jw})=\frac{1}{2}[X(e^{jw})+X^*(e^{-jw})] \qquad X_o(e^{jw})=\frac{1}{2}[X(e^{jw})-X^*(e^{-jw})]\]
以及FT的共轭对称性\[FT[x_r(n)]=X_e(e^{jw}),FT[jx_i(n)]=X_o(e^{jw})\\FT[x_e(n)]=X_R(e^{jw}),FT[x_o(n)]=jX_I(e^{jw})\]
当\(x(n)\)为实序列时\[若x(n)为实偶序列,则X(e^{jw})为实偶函数\\若x(n)为实奇序列,则X(e^{jw})为纯虚奇函数\]
离散时间系统的频率响应
与模拟信号处理中正弦信号和复指数信号具有很重要的作用一样,在数字信号处理中,正弦序列和复指数序列也起着很重要的作用。这是因为线性非移变系统对正弦序列的稳态响应仍然是正弦序列,频率与输入信号频率相同,而幅度和相位取决于系统特性,具体可表述如下
设\(x(n)=e^{jw_0n}\),则\(y(n)=e^{jw_0n}H(e^{jw_0})\),其中\(H(e^{jw_0})\)是系统在\(w_0\)处的频率响应
设\(x(n)=Acos(w_0n+\phi)\)且\(h(n)\)为实序列,则\(y(n)=A|H(e^{jw_0})|cos(w_0n+\phi+\theta)\),其中\(H(e^{jw_0})\)是系统在\(w_0\)处的频率响应,\(\theta=arg[H(e^{jw_0})]\)是系统在\(w_0\)处的相位响应
连续时间信号的取样
取样信号的时域频域表示
取样信号为\(\hat{x_a}(t)=x_a(t)p(t)=\sum_{n=-\infty}^\infty x_a(t)\delta(t-nT),p(t)=\sum_{n=-\infty}^\infty \delta(t-nT)\),其频谱则为\(\\\hat{X_a}(j\Omega)=FT[x_a(t)p(t)]=\frac{1}{2\pi}X_a(j\Omega)*P(j\Omega)=\frac{1}{T}\sum_{r=-\infty}^\infty X_a(j\Omega-jr\Omega_s)\\P(j\Omega)=\frac{2\pi}{T}\sum_{n=-\infty}^\infty\delta(j\Omega-jr\Omega_s)\)
这表明取样信号的频谱就是模拟信号频谱的周期延拓,延拓周期的取样角频率为\(\Omega_s\)
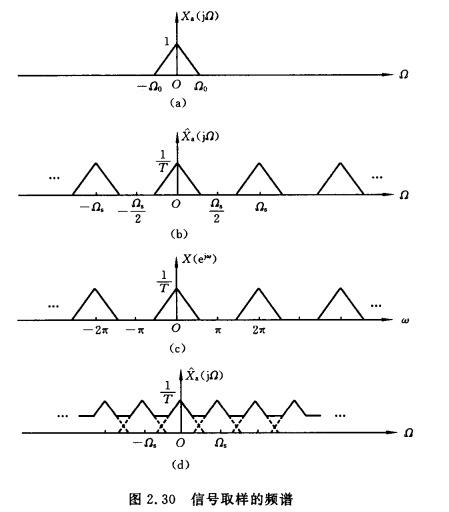
若要不产生混叠,则要求\(\Omega_s\ge2\Omega_0,\Omega_s:奈奎斯特频率,\Omega_s/2\):折叠频率
频率归一化
频率归一化讨论的是离散时间信号\(x(n)\)的频谱\(X(e^{jw})\)和取样信号\(\hat{x_a}(t)\)的频谱\(\hat{X_a}(j\Omega)\)之间的关系
取样信号的频谱为:\[\hat{X_a}(j\Omega)=FT[\hat{x_a}(t)]=FT[x_a(t)p(t)]=FT[\sum_{n=-\infty}^\infty x_a(t)\delta(t-nT)]\\=\sum_{n=-\infty}^\infty x_a(nT)\cdot FT[\delta(t-nT)]=\sum_{n=-\infty}^\infty x_a(nT)e^{-j\Omega nT}\]
而离散时间信号的FT变换为: \[X(e^{jw})=\sum_{n=-\infty}^\infty x(n)e^{-jwn},when \quad w=\Omega T,X(e^{jw})|_{w=\Omega T}=\sum_{n=-\infty}^\infty x(n)e^{-j\Omega Tn}=\hat{X_a}(j\Omega)\]
比较可得出\[X(e^{jw})|_{w=\Omega T}=\hat{X_a}(j\Omega)=\frac{1}{T}\sum_{r=-\infty}^\infty X_a(j\Omega-jr\Omega_s)\\=\frac{1}{T}\sum_{r=-\infty}^\infty X_a(j\frac{w}{T}-jr\frac{2\pi}{T})\]
即在\(w=\Omega T\)的条件下,离散时间信号的频谱与取样信号的相等,由于\(w=\Omega T=\frac{2\pi f}{f_s}(f_s为取样频率)\)是\(f\)对\(f_s\)归一化的结果,因此可认为离散时间信号频谱是模拟信号频谱的周期延拓且在频率轴上进行归一化的结果
信号重建
如果取样信号频谱不存在混叠,让取样信号通过一理性低通滤波器,其特性为\(H(j\Omega)=\begin{cases} T,|\Omega|\le\Omega_s/2\\ 0,|\Omega|>\Omega_s/2 \end{cases}\),其频谱特性为\(H(j\Omega)\hat{X_a}(j\Omega)=X_a(j\Omega),|\Omega|\le\Omega_s/2\),输出信号则为\[x_a(t)=\frac{1}{2\pi}\int_{-\frac{\Omega_s}{2}}^{\frac{\Omega_s}{2}} X_a(j\Omega)e^{j\Omega t}\, {\rm d}\Omega=\sum_{n=-\infty}^\infty x(nT)\cdot S_a(t-nT)\\Sa(t-nT)=\frac{sin[\frac{\pi}{T}(t-NT)]}{\frac{\pi}{T}(t-nT)}为内插函数\]此处积分的详细步骤略过,结论:取样信号经过理想LPF后,完全可以把信号还原,而不损失任何信息,由于插值的唯一性,还原的信号也是唯一的
离散时间信号的取样
其思路与连续时间信号取样类似
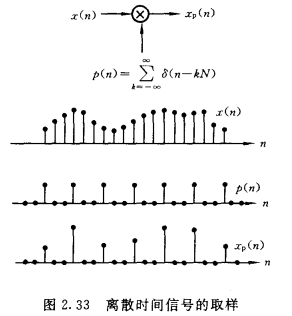
其可以看为一个信号调制的过程:\(x_p(n)=\sum_{n=-\infty}^\infty x(Nk)\delta(n-kN)\),频域表示为\(X_p(w)=\frac{1}{N}\sum_{n=0}^{N-1}X(w-kw_s),w_s\)为取样频率,且\(w_s=\frac{2\pi}{N}\) 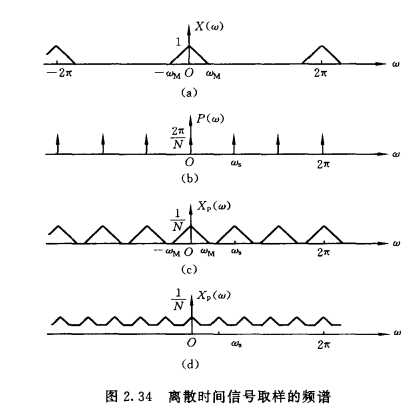
为了不发生混叠,取样频率同样需满足\(w_s\ge2w_M\)
若要恢复序列\(x(n)\),同样可以采用低通滤波器滤波恢复,其频率特性为\(H(w)=\begin{cases} N,|w|\le w_s/2\\ 0,|w|> w_s/2 \end{cases}\),恢复的序列\(x_r(n)=\sum_{k=-\infty}^\infty x(kN)\frac{N}{\pi(n-kN)}sin[\frac{w_s}{2}(n-kN)]\)
离散时间信号的取样和内插
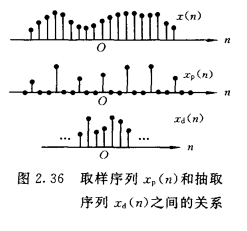
离散时间信号的抽取/减取样:
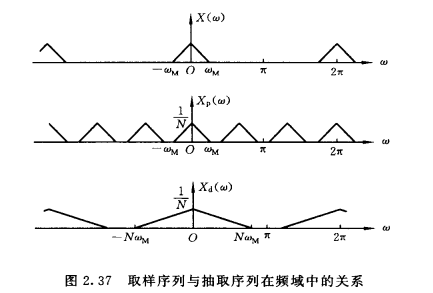
\(x_d(n)=x(nN)=x_p(nN)\\FT(x_d(n))=X_d(w)=\sum_{n=-\infty}^\infty x_p(n)e^{-jwn/N}\\=X_p(w/N)=\sum_{n=-\infty}^\infty x_p(nN)e^{-jwn}\)
取样序列和抽取序列的频谱只是频率尺度不同,注意,只有对原连续时间信号取样率高于奈奎斯特频率,即进行"过采样",才允许进一步降低采样率,即进行“减采样”
离散时间信号的内插/增采样:是抽取的逆过程,现在每相邻两个序列之间插入N-1个零值,再用低通滤波器得到内插后序列 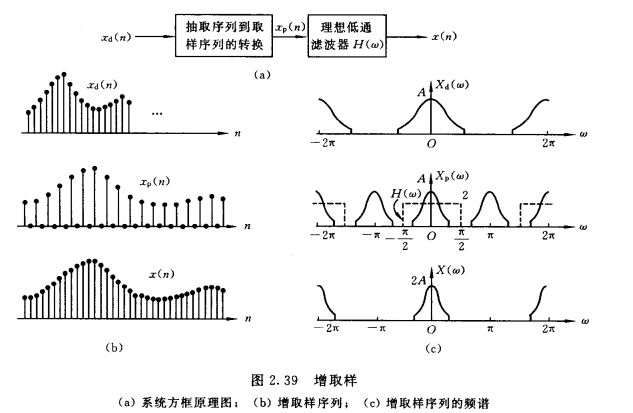
全通系统和最小相位系统
- 全通系统:全通系统是幅度响应\(|H(e^{jw})|\equiv C\)(C为常数)的系统,系统函数:\(H_{ap}(z)=\frac{z^{-1}-a^*}{1-az^{-1}}\)(一阶系统),对于单位取样为实数的多阶系统,有\(H_{ap}(z)=A\prod^M_c\frac{z^{-1}-d_k}{1-d_kz^{-1}}\prod^M_r\frac{(z^{-1}-e_k^*)(z^{-1}-e_k)}{(1-e_kz^{-1})(1-e_k^*z^{-1})},|d_k|,|e_k|<1\),全通系统的特点是每个极点\(z_p\)都有一个与之配对的共轭倒数零点\(z_o=\frac{1}{z_p^*}\),且一阶全通滤波器的相位响应单调递减
- 最小/大相位系统:系统函数\(H_{min}(z)\)所有零极点都在单位圆内/外的系统,对于最小相位系统,存在一个稳定的因果逆系统\(H_{min}^{-1}(z)\),使得\(H_{min}(z)H_{min}^{-1}(z)=1\)
- 全通系统与最小相位系统级联:任何系统可表述为一个最小相位系统和一个全通系统级联,\(H(z)=H_{min}(z)H_{ap}(z)\)
- 相位延迟与群延迟:数字滤波器的相位延迟:\(T_p(w)=-\frac{\phi(w)}{w}\)表示输入是频率为\(w\)的单一正弦波的延迟时间,群延迟则定义为\(T_g(w)=-\frac{d\phi(w)}{dw}\)表示某一频率\(w\)邻域内的延迟性质