前言
本知识小结只针对华中科技大学电子信息与通信学院课程《通信电子线路》进行总结，不保证满足所有读者需求
本章知识小结
概述
本章主要讨论自激式振荡器，它是在无须加激励信号的情况下，能将直流电能转换为具有一定波形、频率、幅度的交变能量电路。振荡器又可根据波形不同分为正弦波振荡器和非正弦波振荡器。正弦波振荡器根据工作方式不同又可分为反馈型振荡器和负阻型振荡器。反馈型振荡器主要由决定振荡频率的选频网络和维持振荡的正反馈放大器组成，本章主要讨论反馈型正弦波振荡器
反馈式振荡器的基本工作原理
反馈式振荡器由反馈放大器演变而来，根据下图可以分析器起振的物理过程和基本组成，简单来说，当开关拨向1，电路未调谐放大器，若在电路稳定后，迅速将开关拨向2点。这是调谐放大器就变为自激振荡器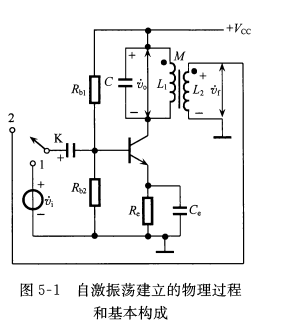 
由自激振荡建立的过程可知，反馈型自激振荡器的电路构成必须由以下三部分组成：
- 包含两个(或以上)储能元件的振荡回路，这两个元件中，一个释放能量时，另一个就接收能量。释放和接收能量可以往返进行，其频率取决于元件数值。
- 可以补充由振荡回路电阻产生损耗的能量来源，在晶体管振荡器中，能源就是直流电源\(V_{CC}\)
- 使能量在正确的时间内补充道电路中的控制设备，由有源器件和正反馈电路完成。
在上述分析中，反馈式振荡器至少包含一个基本放大器和把能量一部分反馈到放大器输入端的反馈网络F。由模电知识可知，反馈环闭环增益表示为:\[\dot{A_f}=\frac{\dot{A_o}}{1-\dot{A_o}\cdot \dot{F}}\] \(\dot{A_o}=\frac{\dot{V_o}}{\dot{V_i}}|_{\dot{V_f}=0}\)为基本放大器小信号开环增益，\(\dot{F}=\frac{\dot{V_f}}{\dot{V_i}}\)为反馈网络小信号电压反馈系数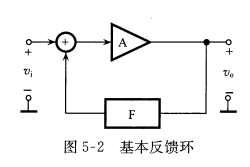 
反馈型正弦波的起振条件为\[\dot{A_o}\dot{F}>1({A_o}F>1.\phi_A+\phi_F=2n\pi,n=0,\pm1,\dots)\]上式为振幅起振条件和相位起振条件，放大器增益A和输出电压幅度\(V_o\)的关系称为振荡特性,\(\frac{1}{F}\)与\(V_o\)之间的关系称为反馈特性，起振的幅度条件如下图所示 
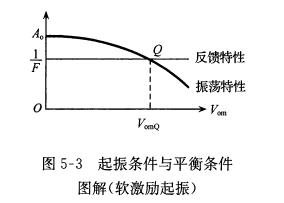但在实际设计中，由于静态工作点太低，振荡器电路无法自行起振，必须给一个较大幅度的初始激励，使动态点越过不稳定平衡点B才能起振，这称为硬激励起振，设计电路时要尽量避免 
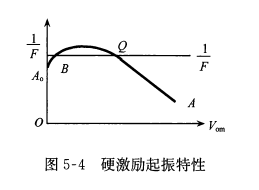起振后，为了确保维持自激振荡，必须满足平衡条件，平衡条件可表述为：\[A\cdot F=1,\phi_A+\phi_F=2n\pi,n=0,1,2\dots\]
若用电路参数表示振幅平衡条件和相位平衡条件则有 \[|\overline{y_{fe}}|\cdot|Z_{p1}|\cdot F=1\\\phi_Y+\phi_Z+\phi_F=2n\pi,n=0,1,2...\]
振荡器平衡状态的稳定条件是指在外因作用下平衡条件被破坏后，振荡器能自动恢复到原来平衡状态的能力，稳定条件也分为振幅稳定和相位稳定两种： 1. 振幅稳定:在平衡点附近，放大倍数随振幅的变化特性具有负的斜率\[\frac{\partial A}{\partial V_{om}}|_{V_{om}=V_{omQ}}<0\] 2. 相位稳定：振荡器相位稳定条件要求谐振回路的相频特性曲线\(\phi_z=f(w)\)在工作频率附近具有负的斜率\[\frac{\partial \phi}{\partial w}\approx\frac{\partial \phi_Z}{\partial w}<0\]
反馈型LC振荡器线路
采用LC谐振回路作为选频网络的反馈振荡器统称为LC振荡器。LC振荡器按其反馈网络的不同，可分为互感耦合振荡器、电感反馈式振荡器和电容反馈式振荡器三种类型，其中后两种通常统称为三端式振荡器
互感耦合振荡器
互感耦合振荡器是依靠线圈之间的互感耦合实现正反馈的，因此，耦合线圈同名端的正确位置至关重要。同时,耦合量M要选择合适,使其满足振幅起振条件。
互感耦合振荡器有三种形式:调集电路、调基电路和调发电路，具体根据振荡回路是在集电极电路、基极电路和发射极电路来区分的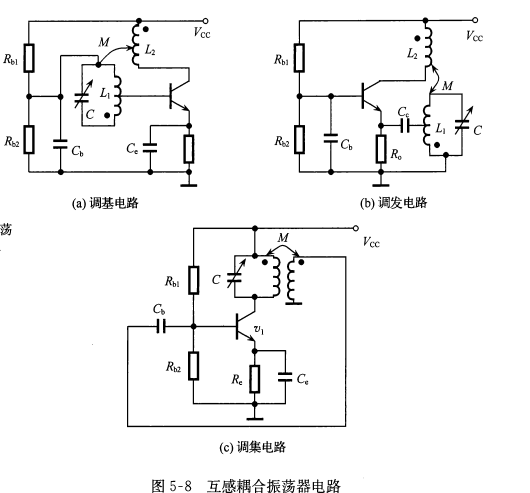 
由于基极和发射极之间的输入阻抗比较低，为了避免过多地影响回路的Q 值，故在调基和调发这两个电路中，晶体管与振荡回路进行部分耦合。调集电路在高频输出方面比其他两种电路稳定,而且幅度较大,谐波成分较小。调基电路振荡频率在较宽的范围改变时，振幅比较平稳。
互感耦合振荡器在调整反馈（改变M）时，基本上不影响振荡频率。但由于分布电容的存在,在频率较高时，难于做出稳定性高的变压器。因此，它们的工作频率不宜过高，一般应用于中、短波波段
根据h 参数等效电路分析可知互感耦合振荡器的振荡频率 \[f_o\approx\frac{1}{2\pi}\sqrt{\frac{1}{LC}}\]
三端式振荡器
1 .电感反馈三端式振荡器（哈特莱电路）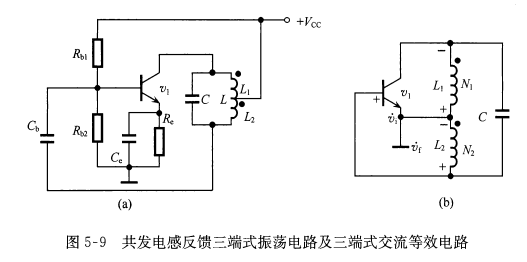 
- 线路特点：它的反馈电压\(\dot{v_f}\)是由电感\(L_2\)上获得的，晶体管的三个电极分别与回路电感的三个端点相连接，故称为电感反馈三端式振荡器。电路中集电极馈电采取串联馈电方式，基极则采取并联馈电方式, \(C_b\)为隔直流电容，防止\(V_{CC}\)通过电感， 加到基极，以免高压击穿管子。
- 振荡频率与反馈系数：\[f_o\approx\frac{1}{2\pi}\sqrt{\frac{1}{LC}}\\L=L_1+L_2+2M，F=\frac{L_2+M}{L_1+M}\]
- 电路的优缺点：优点：\(L_1,L_2\)之间有互感，反馈较强，容易起振;振荡频率调节方便,只要调整电容C的大小即可，而且C的改变基本上不影响电路的反馈系数。缺点:振荡波形不好，因为反馈电压是在电感上获得的，而电感对高次谐波呈高阻抗，因此对高次谐波的反馈较强，使波形失真大;另外，电感反馈三端电路的振荡频率不能做得太高，这是因为频率太高, L太小,不宜制造且分布参数的影响太大。电感三端式振荡器的工作频率一般在几十兆赫兹以下。
- 电容反馈三端式振荡器(考比次电路)
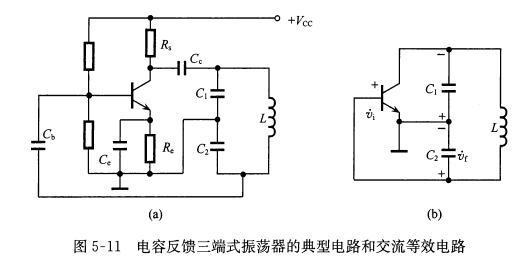
- 线路特点：它的反馈电压\(\dot{v_f}\)是由电容\(C_2\)上获得的，晶体管的三个电极分别与回路电容的三个端点相连接，故称为电容反馈三端式振荡器。电路中集电极和基极均采取并联馈电方式。\(C_b,C_c\)均为隔直电容。
- 振荡频率与反馈系数：\[f_o\approx\frac{1}{2\pi}\sqrt{\frac{1}{LC}}\\C=\frac{C_1C_2}{C_1+C_2},F=\frac{C_1}{C_2}\]
- 电路的优缺点：优点：振荡波形好，因为它的反馈电压\(\dot{v_f}\)是靠电容获得的，而电容元件对信号的高次谐波呈低阻抗，因此，对高次谐波反馈较弱,使振荡波形更接近正弦波;另外,这种电路的频率稳定度较高，由于电路中的不稳定电容均与回路电容\(C_1,C_2\)相并联,因此，适当加大回路的电容量，就可以减小不稳定因素对振荡频率的影响。电容三端电路的工作频率可以做得较高，因为它可直接利用振荡管的输出、输入电容作为回路的振荡电容。它的工作频率可做到几十兆赫兹到几百兆赫兹的甚高频波段范围。缺点:调\(C_1\) 或\(C_2\) 来改变振荡频率时,反馈系数也将改变。但只要在L两端并上一个可变电容器，并令\(C_1\)与\(C_2\)为固定电容，则在调整频率时,基本上不会影响反馈系数。
三端式LC振荡器组成法则（相位平衡条件的判断准则）
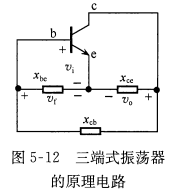电路要振荡必须满足条件：\[x_{be}+x_{ce}+x_{cb}=0\]且由电路分析可以得到，为了满足正反馈条件，\(x_{eb},x_{ce}\)必须性质相同，为同名电抗，\(x_{cb}\)则为异名电抗，以此准则可以迅速判断振荡电路组成是否合理，能否起振
串联型改进电容三端式振荡器(克拉泼电路)
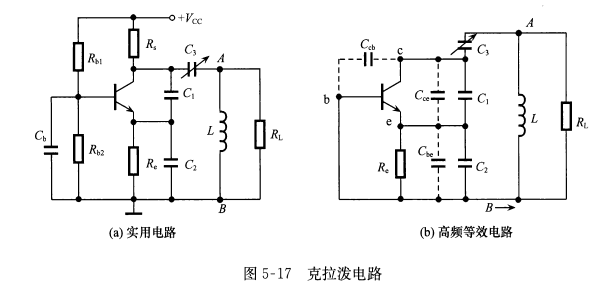与电容三端式电路比较，克拉泼电路的特点是在回路中增加了一个与L串联的电容\(C_3\)。各电容取值必须满足：\(C_3<<C_1,C_3<<C_2,C_3\)为可变电容。这样可使电路的振荡频率近似只与\(C_3,L\)有关。该电路的振荡频率为\[f_o\approx\frac{1}{2\pi}\sqrt{\frac{1}{LC_3}}\]可见，该电路的振荡频率几乎与\(C_1,C_2\)无关，所以克拉泼电路的频率稳定性比电容三端式要好，其缺点为不适于用作波段振荡器。所以克拉泼电路只适于用作固定频率振荡器或波段覆盖系数较小的可变频率振荡器并联型改进电容三端式振荡器(西勒电路)
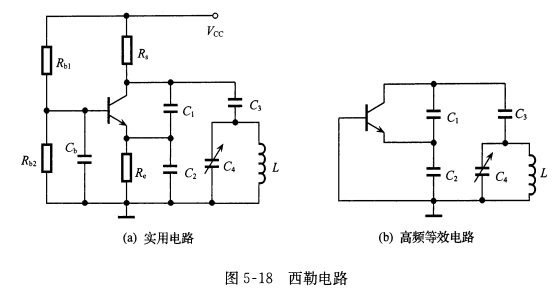西勒电路是在克拉泼电路基础上,在电感L两端并联了一个小电容\(C_4\),且满足\(C_1,C_2\)远大于\(C_3\) ，所以其回路等效电容\[C=\frac{C_1C_2C_3}{C_1C_2+C_2C_3+C_1C_3}+C_4\approx C_3+C_4\] 振荡频率为:\[f_o\approx\frac{1}{2\pi}\sqrt{\frac{1}{LC}}\\C=C_3+C_4\]在西勒电路中，由于\(C_4\)与L并联，所以\(C_4\)大小不影响回路接入系数，在振荡频率变化时基本保持不变，从而使输出振幅稳定，因此其可用作波段振荡器
振荡器的频率稳定问题
振荡器的频率稳定度是振荡器的一个关键指标。频率稳定，就是在各种外界条件发生变化的情况下，要求振荡器的实际工作频率与标称频率间的偏差及偏差的变化最小。评价振荡器频率的主要指标有两个,即准确度与稳定度。
振荡器的实际工作频率f与标称频率\(f_0\)之间的偏差，称为振荡频率的准确度。它通常分为绝对频率准确度与相对频率准确度两种，其表达式如下。 \[绝对准确度：\Delta f=|f-f_0|\\相对准确度：\frac{\Delta f}{f_0}=\frac{|f-f_0|}{f_0}\]
振荡器的频率稳定度则是指在一定时间间隔内，由于各种因素变化，引起的振荡频率相对于标称频率变化的程度\[频率稳定度：\delta=\frac{\Delta f_{max}}{f_0}|_{t=\Delta t}\]
石英振荡器
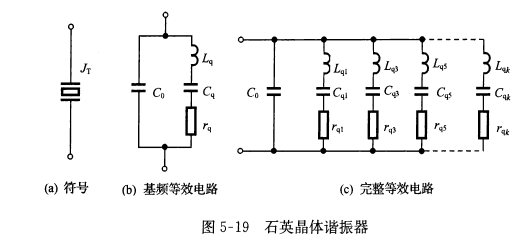上图是石英晶振的符号和等效电路，石英晶振的Q值和特性阻抗\(\rho\)都非常高。这是因为其\(L_q\)较大，\(C_q\)与\(r_q\)很小的缘故。
由上图(b)可知，石英晶振可等效为一个串联谐振回路和一个并联谐振回路，若忽略\(r_q\),则晶振两端呈现纯电抗，其电抗频率特性曲线如下图实线所示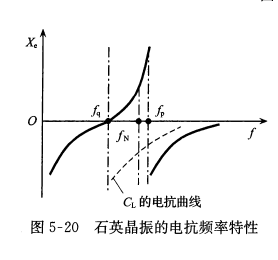 
其串联谐振频率为\(f_q=\frac{1}{2\pi\sqrt{L_qC_q}}\),并联谐振频率为\(f_p=\frac{1}{2\pi\sqrt{L_q\frac{C_0C_q}{C_0+C_q}}}\\=\frac{f_0}{\sqrt{\frac{C_0}{C_0+C_q}}}=f_q\sqrt{1+\frac{C_q}{C_0}}\)
由于\(C_q/C_0\)很小，所以\(f_p,f_q\)间隔很小，因而在\(f_p-f_q\)感性区间, 石英晶振具有陡峭的电抗频率特性，曲线斜率大，利于稳频。若外部因素使谐振频率增大，则根据晶振电抗特性,必然使等效电感L增大，但由于振荡频率与L的平方根成反比,所以又促使谐振频率下降,趋近于原来的值。
晶体谐振器电路
将石英晶振作为高Q 值谐振回路元件接入正反馈电路中，就组成了晶体振荡器。根据石英晶振在振荡器中的作用原理，晶体振荡器可分成两类:一类是将其作为等效电感元件用在三端式电路中，工作在感性区间，称为并联型晶体振荡器;另一类是将其作为一个短路元件串接于正反馈支路上,工作在它的串联谐振频率上，称为串联型晶体振荡器
自问自答
如何化简正弦波振荡器电路？ 在正弦波振荡电路中我们考虑的往往是正反馈产生振荡的电路，因此在简化电路的过程中只需要聚焦正反馈部分即可。不妨对振荡电路中的R、L、C分别讨论。 对于R，在电路化简过程中我们认为其开路，因为R在电路中起到的作用与正反馈无关。 对于L，在高频电路中L的阻抗\(jwL\)很高，尤其是L充当高频扼流圈时往往认为L开路。 对于C，在高频电路中C的阻抗\(\frac{1}{jwL}\)很低，尤其是C充当旁路电容、耦合电容、电源滤波电容时往往认为C短路。
为什么要对电容反馈三端式振荡电路进行改进呢？ 当我们利用电容反馈三端式电路，调\(C_1\)或\(C_2\)来改变振荡频率时，由于反馈系数为\(\frac{C_1}{C_2}\)，易知反馈系数将改变。但是如果给电路串联一个小电容\(C_3\)，因为C3远远小于C1和C2，所以三电容串联后的等效电容可以约等于\(C_3\)。此时振荡角频率和反馈系数独立，可以有效调整并控制电路。\[w_0\approx\frac{1}{LC_3},F=\frac{C_1}{C_2}\]
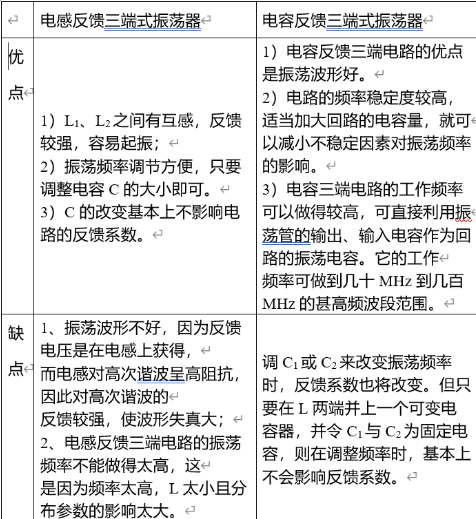
电感反馈三端式振荡器与电容反馈三端式振荡器各有何优缺点？
未解答的疑惑
- 对泛音晶体振荡电路的原理不太理解。
- 石英振荡器的作用和设计思路不理解
参考资料
- 《通信电子线路》（第三版）：严国平，龙占超
- 老师课件
- 通信电子线路mooc