引言
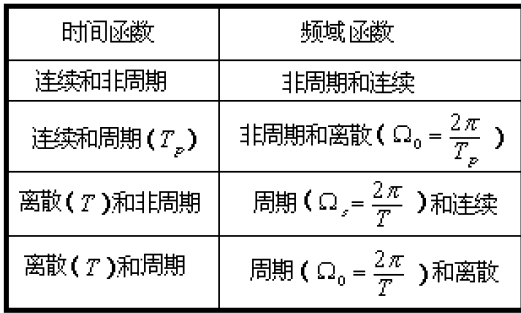
- 连续傅里叶变换(FT)：连续时间,连续频率的傅里叶变换
- 傅里叶级数(FS)：连续时间,离散频率的傅里叶变换
- 序列的傅里叶变换(DTFT):离散时间,连续频率的傅里叶变换
- 离散傅里叶变换(DFT):离散时间,离散频率的傅里叶变换
前三种变换总有一个域不是离散的，计算机不能直接计算；希望的变换：不仅在时间域上离散，在频率域上也离散(DFT)
离散时间信号级数及其性质(DFS)
离散傅里叶级数(DFS)
周期序列表示
\[ 1.\widetilde{x}(n)=\widetilde{x}(n+kN)\\\widetilde{x}(n)=x((n))_N\\\widetilde{x}(n)=\sum_{r=-\infty}^\infty x(n-rN) \]
其中k,r为任意整数，N-周期，其ZT不收敛
在《信号与线性系统》中，用傅里叶级数表示连续时间周期信号。对应地，可用离散傅里叶级数表示离散周期序列，即用周期为N的复指数序列来表示
\[ \widetilde{x}(n)=\frac{1}{N}\sum_{k=0}^{N-1}\widetilde{X}(k)e^{j\frac{2\pi}{N}kn} \]
两边\(\times e^{-j\frac{2\pi}{N}nr}\)并从0-N-1求和并交换左右求和次序得：
\[ \sum_{k=0}^{N-1}\widetilde{x}(n)e^{-j\frac{2\pi}{N}nr}=\widetilde{X}(r) \]
用k置换r 得到
\[ \sum_{k=0}^{N-1}\widetilde{x}(n)e^{-j\frac{2\pi}{N}nk}=\widetilde{X}(k) \]
设\(W_N=e^{-j\frac{2\pi}{N}}\)(旋转因子)，可得周期序列的傅里叶级数变换对
\[ \widetilde{x}(n)=IDFS[\widetilde{X}(k)]=\frac{1}{N}\sum_{k=0}^{N-1}\widetilde{X}(k)W_N^{-kn},-\infty<n<\infty\\\widetilde{X}(k)=DFS[\widetilde{x}(n)]=\sum_{k=0}^{N-1}\widetilde{x}(n)W_N^{kn},-\infty<k<\infty \]
注：\(\widetilde{x}(n),\widetilde{X}(K)\)都是离散和周期性的,且周期为N,DFS只取k次谐波分量中N个谐波分量；n为离散时间变量，理解为nT；k是离散频率变量，理解为\(\Delta wk\),DFS和IDFS具有唯一性
离散傅里叶级数的性质
线性性
周期序列的移位： \[ 设DFS[\widetilde{x}(n)]=\widetilde{X}(k),则：DFS[\widetilde{x}(n-m)]=W_N^{mk}\widetilde{X}(k)\\IDFS[\widetilde{X}(k-l)]=W_N^{-nl}\widetilde{x}(n) \]
周期卷积：设\(\widetilde{x_1}(n),\widetilde{x_2}(n)\)都为周期为N的周期序列，且 \[ \widetilde{X_1}(k)=\sum_{m=0}^{N-1}\widetilde{x_1}(m)W_N^{km},\\\widetilde{X_2}(k)=\sum_{r=0}^{N-1}\widetilde{x_1}(m)W_N^{kr},\\\widetilde{Y}(k)=\widetilde{X_1}(k)\widetilde{X_2}(k),\\则\widetilde{y}(n)=IDFS[\widetilde{X_1}(k)\widetilde{X_2}(k)]=\sum_{m=0}^{N-1}\widetilde{x_1}(m)\widetilde{x_2}(n-m) \]
结论：周期卷积的操作步骤与非周期序列的线性卷积相同，不同的是周期卷积仅在一个周期内求和。周期卷积中\(\widetilde{x_1}(m),\widetilde{x_2}(n-m)\)对m是周期性的，周期为N,\(\widetilde{y}(n)\)周期为N,且周期卷积满足交换律
同理可得：如果\(\widetilde{y}(n)=\widetilde{x_1}(n)\widetilde{x_2}(n)\),则有\(\widetilde{Y}(k)=DFS[\widetilde{x_1}(n)\widetilde{x_2}(n)]=\frac{1}{N}\widetilde{X_1}(k)*\widetilde{X_2}(k)\)
离散傅里叶变换及其性质
有限长序列的Fourier变换称为离散Fourier变换(DFT)，定义方法：由DFS导出DFT。
- 将有限长序列\(x(n)\)延拓成周期序列\(\widetilde{x}(n)\)
- 求周期序列\(\widetilde{x}(n)\)的DFS得\(\widetilde{X}(k)\)
- 取出\(\widetilde{X}(k)\)的一个周期作为\(x(n)\)的DFT \[ X(k)=\widetilde{X}(k)R_N(k) \]
经由上诉步骤可由DFS得出有限长序列的DFT为
\[ x(n)=IDFT[X(k)]=\frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{j\frac{2\pi}{N}kn}=\begin{cases} \frac{1}{N}\sum_{k=0}^{N-1}X(k)W_N^{-kn},0\le n\le N-1\\ 0,others \end{cases}\\ X(k)=DFT[x(n)]=\sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}kn}=\begin{cases} \sum_{n=0}^{N-1}x(n)W_N^{kn},0\le k\le N-1\\ 0,others \end{cases} \]
注：\(x(n),X(K)\)都是有限长的，取值范围为\(0\sim N-1\),n为离散时间变量，理解为nT,k是离散频率变量，理解为\(\Delta wk\),DFT与DFS无本质区别，DFT是DFS的主值，且隐含周期性，具有唯一性。
用矩阵计算N点DFT
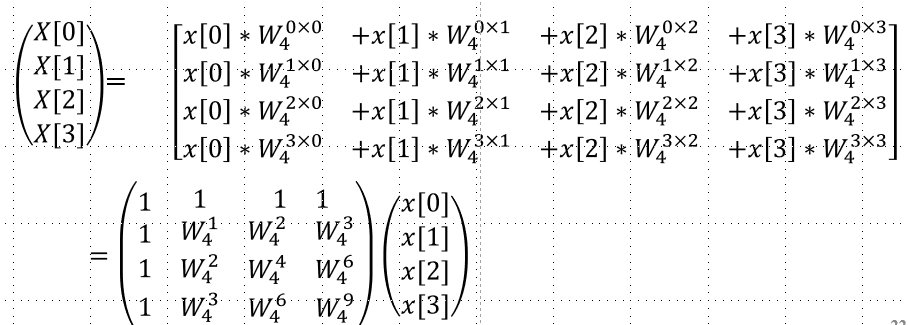
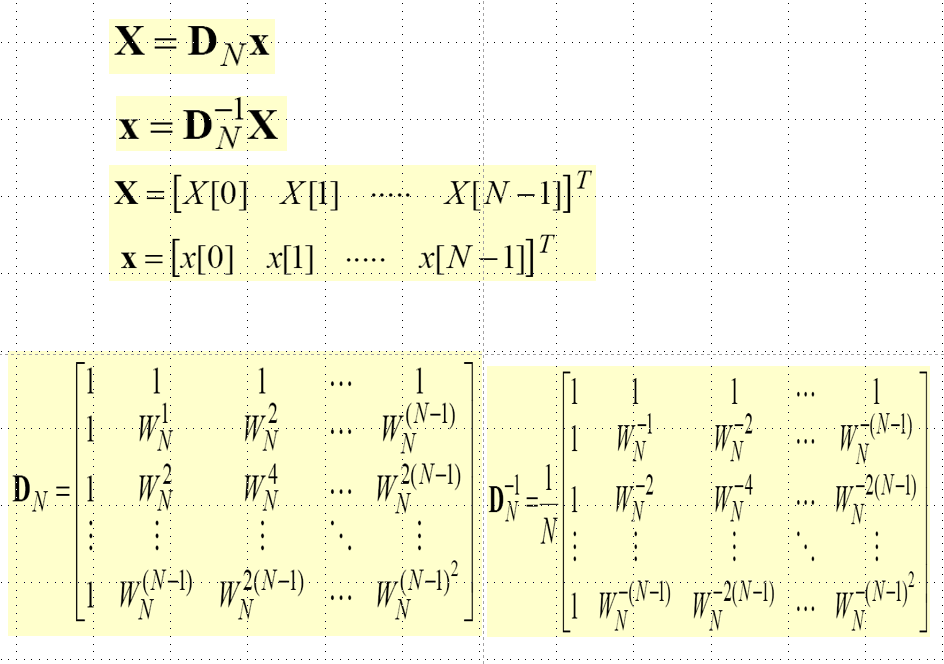
DFT的性质
旋转因子的性质
- 对称性：\((W_N^k)^*=W_N^{N-k}\)
- 周期性：\(W_N^{k+mN}=W_N^k\)
- 换底：\(W_N^k=W_{mN}^{mk}\)
\(\frac{N}{2}，\frac{N}{4}\)点DFT为
\[ X(k)=\sum_{n=0}^{N/2-1}x(n)W_{N/2}^{kn},k=0,1,...,N/2-1\\X(k)=\sum_{n=0}^{N/4-1}x(n)W_{N/4}^{kn},k=0,1,...,N/4-1 \]
DFT与ZT/FT的关系：有限长序列\(x(n)\)的DFT系数\(X(k)\)可看作其ZT在单位圆上等角距取样的样本值:\(X(k)=X(z)|_{z=W_N^{-k}}\),有限长序列\(x(n)\)的DFT系数\(X(k)\)可看作其FT在一个周期\(2\pi\)中等间距取样的样本值，取样间隔\(\Delta w=\frac{2\pi}{N}:X(k)=X(e^{jw})|_{w=\frac{2\pi}{N}k}=X(e^{j\frac{2\pi}{N}k})\)
离散傅立叶变换的性质:
线性
复共轭序列的DFT \(DFT[x^*(n)]=X^*(N-k),0\le k \le N-1\) 由上式可知 \[\begin{cases} Re[X(k)]=Re[X(N-k)]\\ Im[X(k)]=-Im[X(N-k)] \end{cases}\] 进一步可以方便的由一个复序列的DFT求得两个实序列的DFT \[w(n)=x(n)+jy(n)\\W(k)=X(k)+jY(k)=Re[X(k)]-Im[Y(k)]+j(Im[X(k)]+Re[Y(k)])\\\because x(n)=\frac{1}{2}[w(n)+w^*(n)]\qquad y(n)=\frac{1}{2j}[w(n)-w^*(n)]\\\therefore X(k)=\frac{1}{2}[W(k)+W^*(N-k)]\qquad Y(k)=\frac{1}{2j}[W(k)-W^*(N-k)]\]
对称性
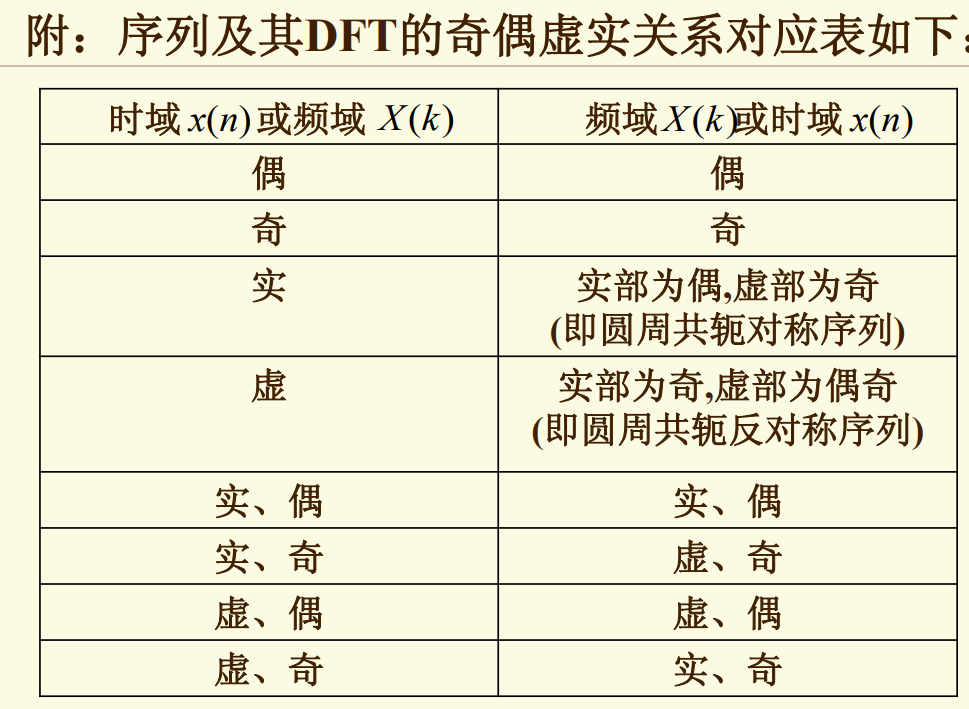
- 有限长共轭对称序列\(x_{ep}(n)=x_{ep}^*(N-n)\),也可称为圆周共轭对称序列。
- 有限长共轭反对称序列\(x_{op}(n)=-x_{op}^*(N-n)\)
- 变换区间：\(0\le n \le N-1\)，以n=N/2为对称点
- 频域定义：共轭对称序列：\(X_{ep}(k)=X_{ep}^*(N-k)\)，共轭反对称序列：\(X_{op}(k)=-X_{op}^*(N-k)\)
- 序列分解：
- \(x_{ep}(n)=\frac{1}{2}[x(n)+x^*(N-n)],x_{op}(n)=\frac{1}{2}[x(n)-x^*(N-n)]\)
- \(DFT[jx_i(n)]=X_{op}(k) \quad DFT[x_r(n)]=X_{ep}(k)\\DFT[x_{ep}(n)]=X_R(k) \quad DFT[x_{op}(n)]=jX_I(k)\)
序列的循环移位:一个序列的循环移位定义为:\(y(n)=x((n+m)_N)\cdot R_N(n)\),序列循环移位后DFT为:\(Y(k)=DFT[x((n+m)_N)R_N(n)]=W_N^{-km}X(k)\),由时域频域的对偶关系，\(X(k)\)循环移位时，设\(Y(k)=X((k+l))_N\cdot R_N(k)\),则\(y(n)=IDFT[X((k+l))_NR_N(k)]=W_N^{nl}x(n)\)
循环卷积:对于两个长度均为N的序列\(x_1(n),x_2(n)\),其循环卷积定义为\(y(n)=\sum_{m=0}^{N-1}x_1(m)x_2((n-m))_NR_N(n)=\)
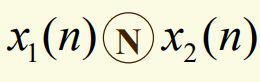特点：- 循环卷积的过程与周期卷积一样，只取周期卷积的主值
- 循环卷积隐含周期性
- 循环卷积在主值区间内进行，参与卷积的两个序列的长度和结果序列的长度均相等
- 线性卷积与循环卷积计算步骤比较：
- 线性卷积：反折、平移、相乘、积分(或相加)
- 循环卷积：反折、周期化、平移、相乘、相加
利用循环卷积计算线性卷积
循环卷积与线性卷积的对比图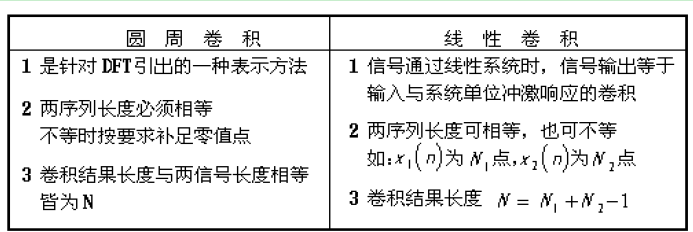 
由循环卷积求线性卷积
- 当\(L<N+M-1\)其循环卷积的结果与线性卷积不相等，但满足一定关系
- 当\(L\ge N+M-1\)两个长度为M，N的序列的线性卷积可用长度均为L的循环卷积来代替
频率取样
序列的几种变换之间的关系
- ZT与FT：\(X(z)|_{z=e^{jw}}=X(e^{jw})\) 单位圆上的ZT等于序列的FT
- LT与ZT：\(X(z)|_{z=e^{sT}}=\hat{X}_a(s)\) S平面->Z平面：S平面上的宽度为\(\frac{2\pi}{T}\)的水平带映射为整个平面，左半带映射到单位圆内，右半带映射成单位圆外，虚轴映射为单位圆
- DFT与ZT：\(X(k)=X(z)|_{z=W_N^{-k}}\) DFT是ZT在单位圆上等角距\(\frac{2\pi}{N}\)取样的样本值
- DFT与FT：\(X(k)=X(e^{jw})|_{w=\frac{2\pi}{N}k}=X(e^{j\frac{2\pi}{N}k})\),DFT是FT在一个周期等间距取样值，取样间隔\(\Delta w=\frac{2\pi}{N}\)
从N个取样值恢复\(x(n)\)
频域取样是指对时域已是离散，频域仍是连续信号。现在频域上进行抽样处理，使其频域也离散化。
在Z平面的单位圆上对序列的ZT进行等角距取样，将导致时间序列的周期延拓 取样后序列主值序列为\(x_N(n)=x_p(n)R_N(n)=[\sum_{r=-\infty}^{\infty}x(n+rM)]R_N(n)\)
对于长度为N的有限长序列，ZT取样即频率取样不失真的条件是取样点数M应等于或大于原序列的长度N
从N个取样值恢复\(X(z),X(e^{jw})\)
长度为N的序列\(x(n)\)的FT\(x(e^{jw})\)可通过Z平面单位圆上的N个取样值\(x(k)\)，即N个频域取样值来恢复,其中用到了和第二章类似的思路通过内插函数\(\phi(z)\)与\(x(k)\)相乘恢复
快速傅里叶变换
直接计算DFT对于计算机来说运算时间和资源占用非常大，因此本节将介绍两种常用的快速傅里叶变换算法(FFT)来用于DFT计算
时间抽取FFT算法
基本出发点：利用\(W_N^k\)的周期性和对称性，将DFT的计算分解成一些逐次减小的DFT计算；
分解规则：：（1）对时间进行偶奇分（2）对频率进行前后分。
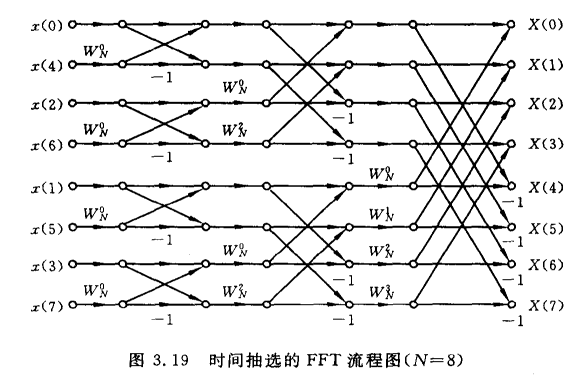
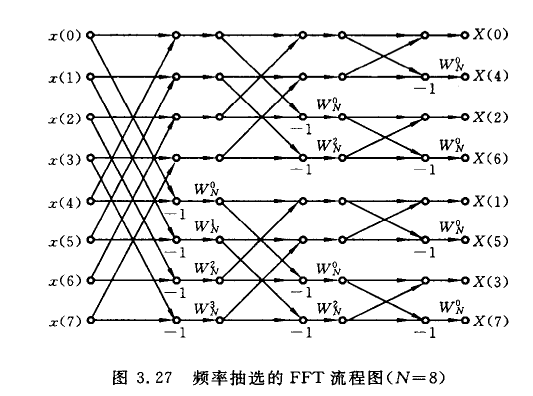
上面时间抽选FFT流图具有三个特点： ① 基本计算单元为一碟形； ② 输入为“混序”排列；输出为正序排列； ③ 具有“同址计算”特性。
- 蝶形计算： 对于任意\(N=2^M\)，总可以通过M级分解成2点DFT计算，每次由\(\frac{N}{2}\)蝶形计算组成，如下图所示
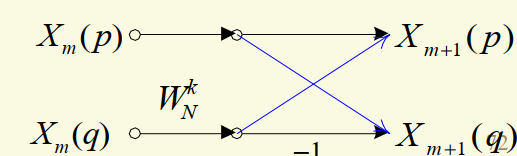计算方程为 \[\begin{cases}
X_{m+1}(p)=X_m(p)+W_N^kX_m(q)\\
X_{m+1}(q)=X_m(p)-W_N^kX_m(q)
\end{cases}\] 完成一次蝶形运算需要2次复加法和1次复乘法，因为完成\(N=2^M\)点的DFT计算需要\(log_2N\)级迭代计算，每级\(\frac{N}{2}\)个蝶形，蝶形数\(\frac{N}{2}log_2N\)，完成N点的时间抽选FFT总计算量为:复乘法次数\(\alpha_F=\frac{N}{2}log_2N\),复加法次数\(\beta_F=Nlog_2N\)，直接计算DFT需复乘法次数\(\alpha_D=N^2\),则\(\frac{\alpha_F}{\alpha_D}=\frac{log_2N}{2N}\) - 同址计算： 蝶形计算的好处在于其是一个蝶形计算，输入的运算结果直接送到下一蝶形计算输入保存，中间不需要其他存储器，节省存储单元，N越大好处越明显
- 变址计算 从FFT流图可知，输入是混序排列，输出是正序排列，在实际计算中，输入的混序是通过输入正序排列按码位倒置的变址处理得到的，即 \[x(1)\rightarrow x(001)\Rightarrow x(100)\rightarrow x(4)\] 这样即可实现FFT的同址计算
频率抽取FFT算法
分解原则：(1)对时间前后分；(2)对频率偶奇分
N为合数的FFT算法
在前面两小节的讨论中，我们只涉及序列长度\(N=2^M\)的FFT算法，本节则将着重讨论如果序列长度\(N\neq2^M\)时的处理办法。通常有以下两种处理方法
- 用补零的办法将\(x(n)\)延长为\(2^M\)，再使用基2FFT算法。由于有限长序列补零以后，只是频谱的取样点有所增加。
- 采用以任意数为基数的FFT算法。设N等于两个整数p和q的乘积，即\(N=p\cdot q\)，则可将N点DFT分解成p个q点DFT或q个p点DFT来计算。
FFT应用
利用FFT对信号进行谱分析
所谓谱分析就是计算信号的频谱，包括振幅谱、相位谱和功率谱。设离散时间信号\(x(n)\)是从连续时间信号\(x_a(t)\)取样得到的，定义参数如下:
- T-取样周期(s)
- \(f_s\)-取样频率(Hz),\(f_s=\frac{1}{T}\)
- \(f_0\)-连续时间信号的最高频率(Hz)
- F-频率分辨率：指频域取样中两相邻点间的频率间隔(Hz)
- \(t_p\)-信号的最小记录长度(s),\(t_p=\frac{1}{F}\)
- N-一个记录长度中的取样数,\(t_p=NT\)
根据取样定理，为了避免混叠失真，要求
\[ f_s\ge2f_0\quad or \quad T\le \frac{1}{2f_0} \]
最小记录长度为：\(t_p=NT=\frac{1}{F}\)，则取样点数N须满足条件\(N\ge\frac{2f_0}{F}\)