引言
滤波器的分类
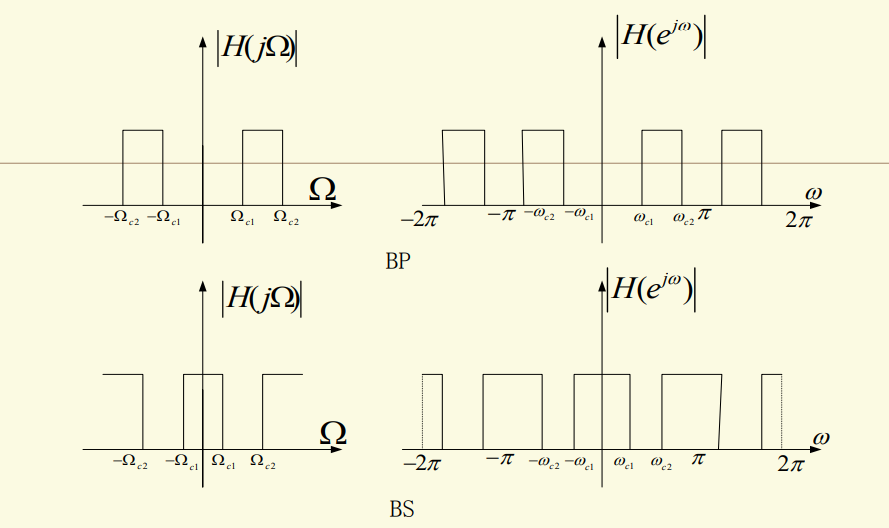
经典滤波器从功能上可分为：低通(LP),高通(HP),带通(BP),带阻(BS),且均有AF和DF之分,AF和DF的四种滤波器的理想幅频响应如下图所示：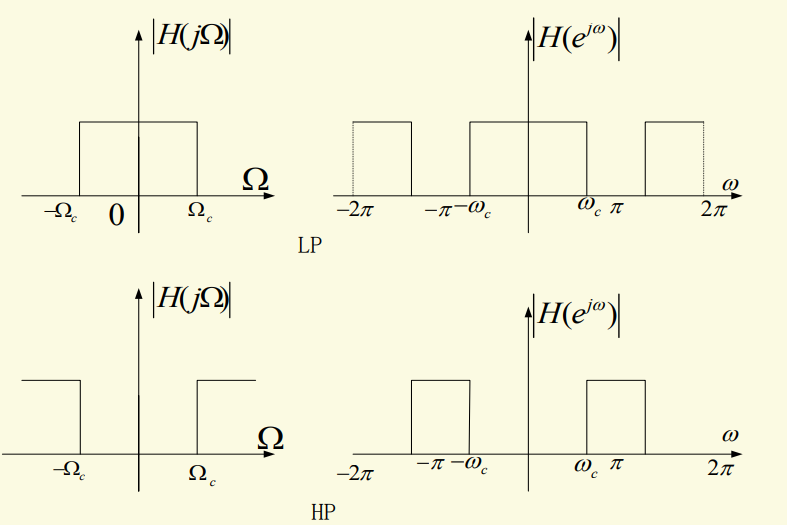 
数字滤波器的技术要求
数字滤波器的传输函数:\(H(e^{jw})=|H(e^{jw})|e^{j\phi(w)}\)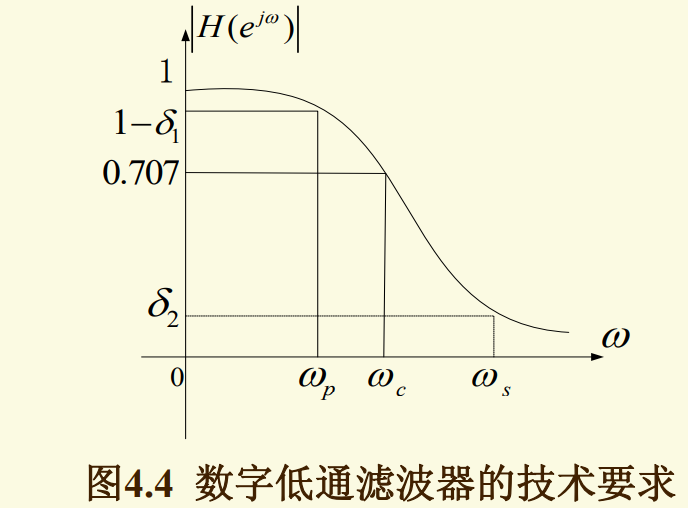 
\(w_p\):通带截止频率, \(\alpha_p\):通带允许的最大衰减
\(w_s\):阻带截止频率, \(\alpha_s\):阻带允许的最小衰减
\(w_c\):3dB通带截止频率，\(\delta_1,\delta_2\)：通带、阻带的容限(允许误差)
\(\alpha_p,\alpha_s\)分别定义为：
\[ \alpha_p=20lg\frac{|H(e^{j0})|}{|H(e^{jw_p})|}\\\alpha_s=20lg\frac{|H(e^{j0})|}{|H(e^{jw_s})|} \]
模拟滤波器的技术要求
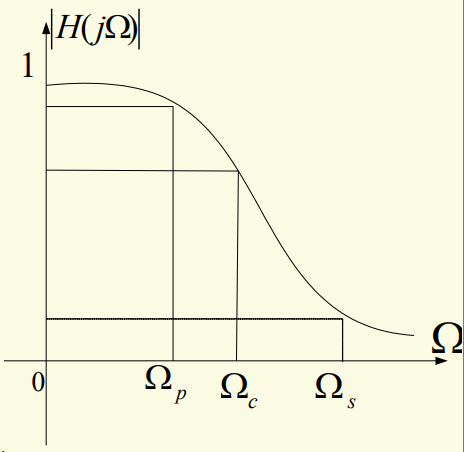
\(\Omega_p\):通带截止频率, \(\alpha_p\):通带中的最大衰减系数
\(\Omega_s\):阻带截止频率, \(\alpha_s\):阻带的最小衰减系数
\(\Omega_c\):3dB通带截止频率
\(\alpha_p,\alpha_s\)分别定义为：
\[ \alpha_p=20lg\frac{|H_a(j0)|}{|H_a(j\Omega_p)|}\\\alpha_s=20lg\frac{|H_a(j0)|}{|H_a(j\Omega_s)|} \]
数字滤波器的三种基本运算的框图表示和流程图表示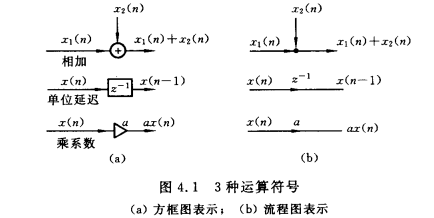 
IIR数字滤波器的基本网络结构
直接I型
系统函数：\(H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^M b_k\cdot z^{-k}}{1-\sum_{k=1}^N a_k\cdot z^{-k}}=H_1(z)\cdot H_2(z)\)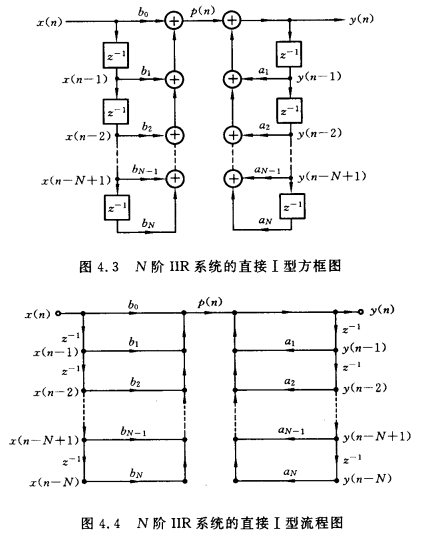 
其中\(H_1(z)=\sum_{k=0}^M b_k\cdot z^{-k},H_2(z)=1/[1-\sum_{k=1}^N a_k\cdot z^{-k}]\)
直接I型,先实现\(H_1(z)\),再实现\(H_2(z)\),特点：先实现系统函数的零点，再实现极点，需要2N个延迟器和2N个乘法器。
直接II型
直接II型,先实现\(H_2(z)\),再实现\(H_1(z)\),特点：先实现系统函数的极点，再实现零点，需要N个延迟器和2N个乘法器。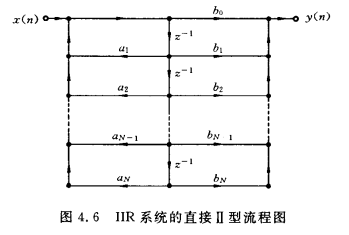 
级联型
系统函数：\(H(z)=A\prod_{k=1}^L \frac{\beta_{0k}+\beta_{1k}\cdot z^{-1}+\beta_{2k}\cdot z^{-2}}{1-\alpha_{1k}\cdot z^{-1}-\alpha_{2k}\cdot z^{-2}}=A\prod_{k=1}^L H_k(z)\),\(H_k(z)\)称为滤波器的二阶基本节。 
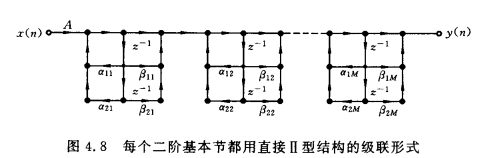
基本结构：二阶基本节，“田字型”结构。特点：1、二阶基本节搭配灵活，可调换次序；2、可直接控制零极点；3、存储器最少；4、误差较大。
并联型
系统函数:\(H(z)=c_0+\sum_{k=1}^P \frac{A_k}{1-c_k\cdot z^{-1}}+\sum_{k=1}^Q \frac{\gamma_{0k}+\gamma_{1k}\cdot z^{-1}}{1-\alpha_{1k}\cdot z^{-1}-\alpha_{2k}\cdot z^{-2}}\)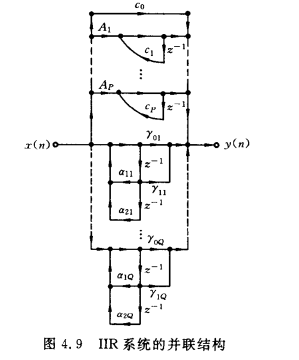 
基本结构：一阶基本节和二阶基本节。特点：1、可单独调整极点，不能直接控制零点；2、误差小，各基本节的误差不相互影响；3、速度快。
FIR数字滤波器的基本网络结构
FIR数字滤波器是一种非递归结构，其冲激响应\(h(n)\)是有限长序列
\[ H(z)=\sum_{n=0}^{N-1} h(n)z^{-n} \]
FIR系统仅在\(z=0\)处有N-1阶极点，在其它地方没有极点，有(N-1)个零点分布在有限Z平面内的任何位置上。
直接型
系统函数:\(H(z)=\sum_{n=0}^{N-1}h(n)z^{-n}=h(0)+h(1)z^{-1}+\dots+h(N-1)z^{-(N-1)}\)
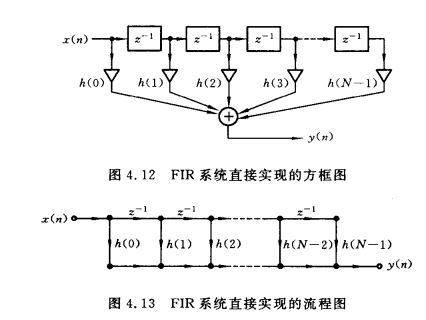
特点：只含前向通路
级联型
系统函数:\(H(z)=\sum_{k=0}^{N-1}h(n)z^{-k}=\prod_{k=1}^M(\beta_{0k}+\beta_{1k}\cdot z^{-1}+\beta_{2k}\cdot z^{-2}),h(n)\)为实系数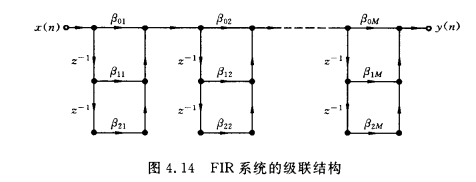 
特点：1、每一个基本节控制一对零点；2、乘法器较多；3、遇到高阶时\(H(z)\)难分解。
快速卷积型
已知两个长度为N的序列的线性卷积，可用2N-1点的循环卷积来代替。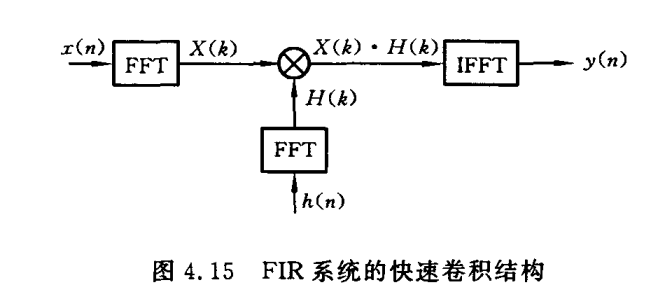 
特点：能对信号进行高速处理。需要实时处理时采用此结构。
线性相位型
- 线性相位FIR DF的条件： 单位取样响应\(h(n)=\pm h(N-1-n),\),当N为奇数时，系统的幅度响应和相位响应为\(\begin{cases} H(w)=\sum_{n=1}^{N/2}a(n)cos[w(n-\frac{1}{2})]\\ \phi(w)=-w(N-1)/2 \end{cases}\)。幅度函数\(H(w)\)是一个标量函数，可以包括正值和负值;\(H(w)\)对\(\pi\)呈奇对称。相位特性是严格线性的。当N为偶数时，系统的幅度响应和相位响应\(\begin{cases} H(w)=\sum_{n=1}^{(N-1)/2}b(n)cos[w(n)]\\ \phi(w)=-w(N-1)/2 \end{cases}\)。\(H(w)\)对\(0,\pi,2\pi\)呈偶对称,相位特性是严格线性的。
- 线性相位FIR DF系统函数的零点分布 零点分布：两组共轭对\(z,\frac{1}{z},z^*,\frac{1}{z^*}\)--要求\(h(n)\)为实序列，如果不为实序列，只能确定零点分布为\(z,\frac{1}{z}\)
- 线性相位FIR DF系统函数的系数特点 冲激响应为偶对称的线性相位系统函数多项式的系数是镜像对称的,如一个四阶系统\(H(z)\)的的形式\(a+bz^{-1}+cz^{-2}+bz^{-3}+az^{-4}\)
- 线性相位FIR DF的网络结构
=h(N-1-n)$且N为偶数时.png)
频率取样型
上章已证明：长度为N的有限长序列的z变换可用围绕单位圆上的N个等间隔的取样值来表示。即 \[X(z)=\frac{1-z^{-N}}{N}\cdot \sum_{k=0}^{N-1}\frac{X(k)}{1-W_N^{-k}\cdot z^{-1}}\] 对FIR系统，其冲激相应\(h(n)\)是有限长的（长度为N），根据上述的插值公式，FIR系统的系统函数可表示为： \[H(z)=\frac{1-z^{-N}}{N}\cdot \sum_{k=0}^{N-1}\frac{H(k)}{1-W_N^{-k}\cdot z^{-1}}\] 其中\(H(k)\)是\(h(n)\)的z变换在各点上的取样值，即 \[H(k)=H(z)|_{z=W_N^{-k}}\] 上式为实现FIR滤波器提供了另一种结构，由两个串联网络组成，即： \[H(z)=\frac{1}{N}H_1(z)\cdot H_2(z)=\frac{1-z^{-N}}{N}\cdot \sum_{k=0}^{N-1}\frac{H(k)}{1-W_N^{-k}\cdot z^{-1}}=\frac{1}{N}H_1(z)\cdot \sum_{k=0}^{N-1} H_k(z)\] 其串联网络如下图所示： 
第一节网络\(H_1(z)\)是由N节延迟线组成的梳状滤波器。
相应的差分方程为\(y_1(n)=x(n)-x(n-N),H_1(z)\)在单位圆上有N个等分零点，即：\(z_k=e^{j\frac{2\pi}{N}k},k=0,1,\dots,N-1\) 其频率响应为：\(H_1(e^{jw})=1-e^{-jwN}\),其流图和幅频特性表示如图：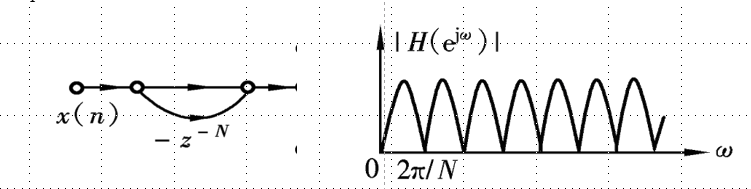 
第二个网络\(H_2(z)=\sum_{k=0}^{N-1} H_k(z)\)是并联的一阶网络,每个一阶网络\(H_k(z)=\frac{H(k)}{1-W_N^{-k}\cdot z^{-1}}\)是一个谐振器,每个一阶网络在单位圆上有一个极点：\(z_k=W_N^{-k}\)
结论： 1. 由N个谐振器并联的网络有N个极点； 2. 网络对\(w=\frac{2\pi}{N},k＝0，1，2，……（N－1）\)的响应为无穷大； 3. 并联谐振器的极点正好各自与梳状滤波器的零点相抵消，从而使这个频率上的响应等于H(k)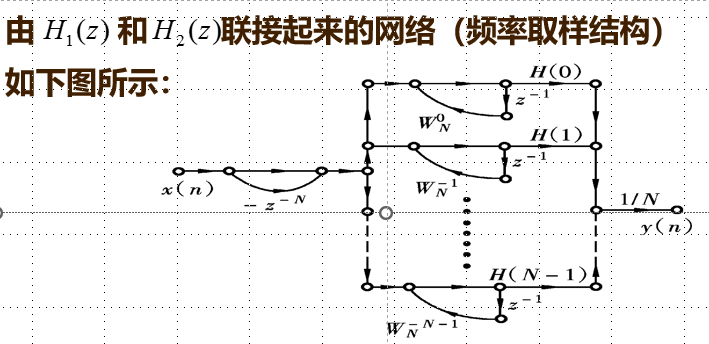 
FIR系统频率取样结构的主要特点是：并联谐振器的系数\(H(k)\)就是滤波器在\(w=\frac{2\pi}{N}k\)处的响应，因此控制其响应是很直接的。
缺点： 1. 所有的相乘系数都是复数，复数乘法比较麻烦； 2. 所有谐振器的极点均在单位圆上，如果滤波器的系数稍有误差，极点就可能移到单位圆外，系统不容易稳定。
改进： 1. 将谐振器的极点从单位圆向内收缩，使极点处在半径为\(r<1\)的圆上，\(H(z)=\frac{1-r^Nz^{-N}}{N}\cdot \sum_{k=0}^{N-1}\frac{H_r(k)}{1-r\cdot W_N^{-k}\cdot z^{-1}}\) 2. 将复数的复乘法运算变成实数相乘，即复一阶网络用实系数的二阶网络来实现
IIR数字滤波器的设计方法
设计步骤：
- 根据实际需要给定滤波器的技术指标。
- 由技术指标计算滤波器的系统函数\(H(z)\)或单位取样响应\(h(n)\)，即用一个稳定的因果系统逼近这些指标；
- 用有限精度的运算实现\(H(z)\)或\(h(n)\)，包括选择运算结构、进行误差分析和选择存储单元的字长。
IIR常用的设计方法：
- 将IIR模拟滤波器映射成数字滤波器 \(H(z)=H_a(s)|_{s=m(z)}\)映射函数\(s=m(z)\)应具有下列性质：
- 将\(s\)平面的虚轴\(j\Omega\)映射成z平面上的单位圆周\(|z|=1\),以保持模拟滤波器的幅度响应在映射后不发生失真。
- 将s平面左半平面映射成z平面单位圆内的内部，以保证稳定的模拟滤波器能够映射成稳定的数字滤波器
- \(m(z)\)是有理函数，将有理函数\(H_a(s)\)映射成有理函数\(H(z)\)
- 计算机辅助设计方法
冲激响应不变法
- 使用冲激响应不变法设计数字滤波器的准则 使数字滤波器的单位取样响应与所参照的模拟滤波器的冲激响应的取样值一样，即\(h(n)=h_a(nT)\)，复频域:\(H(z)|_{z=e^{sT}}=\frac{1}{T}\sum_{r=-\infty}^{\infty}H_a(s-j\frac{2\pi}{T}r)\)。DF与AF的频率特性\(H(e^{jw})|_{w=T\Omega}=\frac{1}{T}\sum_{r=-\infty}^{\infty} H_a(j\frac{w}{T}-j\frac{2\pi}{T}r)\) 数字滤波器的频率响应是模拟滤波器频率响应的周期延拓。在冲激响应不变法中，数字滤波器的频率响应产生混迭失真；数字域频率和模拟域频率之间是线性关系,即\(w=T\Omega\)频率之间不产生失真,且T在设计中是一个无关紧要的参量，常为了方便取1.冲激响应不变法最适合可以用部分分式表示的传递函数
- 冲激响应不变法设计数字滤波器的设计步骤 \(H_a(s)->h_a(t)->h(n)=h_a(nT)->H(z)\)
- 假设模拟滤波器的传递函数\(H_a(s)\)具有单阶极点，且分母的阶数高于分子的阶数,将\(H_a(s)\)展开为部分分式得\(H_a(s)=\sum_{k=1}^N \frac{A_k}{s-s_k}\),\(s_k\)为极点，对\(H_a(s)\)求laplace变换得：\(h_a(t)=\sum_{k=1}^N A_ke^{s_kt}\cdot u(t)\)
- 使用冲激不变法求数字滤波器的冲激响应\(h(n)\) 令\(t=nT\),代入上式得\(h(n)=h_a(nT)=h_a(t)=\sum_{k=1}^N A_ke^{s_knT}\cdot u(nT)\)
- 求\(h(n)\)的z变换得\(H(z)=Z[h(n)]=\sum_{n=0}^\infty[\sum_{k=1}^N A_ke^{s_knT}\cdot ]z^{-n}=\sum_{k=1}^N \frac{A_k}{1-e^{s_kT}z^{-1}}\)
- 冲激响应不变法的应用范围:能够设计的滤波器：LP、BP；
双线性变换法
- 双线性变换法设计数字滤波器 双线性变换法是一种s平面到z平面的映射过程，定义为\(s=\frac{2}{T}\cdot\frac{1-z^{-1}}{1+z^{-1}}\),故有\(H(z)=H_a(s)|_{s=\frac{2}{T}\cdot\frac{1-z^{-1}}{1+z^{-1}}}=H_a(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}})\) 将\(z=e^{jw}\)和\(s=j\Omega\)带入得\(s=\frac{2}{T}\cdot \frac{1-z^{-1}}{1+z^{-1}}:j\Omega=\frac{2}{T}\cdot\frac{1-e^{-jw}}{1+e^{jw}}=\frac{2}{T}\cdot jtan(w/2)\),即\(w=2arctan(\frac{T\Omega}{2})\)
- 数字域频率和模拟域频率之间是非线性关系,当\(\Omega\)从\(0->+\infty,w:0->\pi\)。即：AF的全部频率特性，被压缩成等效于DF在频率\(0<w<\pi\)之间的特性。
- 幅度上无混迭失真。双线性变换的频率标度的非线性失真可以通过预畸变的方法来补偿。设所求的数字滤波器的通带和阻带的截止频率分别为\(w_p\)和\(w_s\),则
- 双线性变换是简单映射；
- 双线性变换是稳定的变换；即模拟滤波器在s平面左半平面的所有极点经映射后均在z平面的单位圆内。
- 双线性变换法设计数字滤波器的设计步骤 模拟低通滤波器->双线性变换映射成数字低通滤波器->数字低通滤波器的频率响应。
- 双线性变换法的应用范围：能够设计的滤波器－LP、HP、BP、BS。
- 冲激响应不变法和双线性变换法比较：
- 相同点：首先设计AF，再将AF转换为DF。
- 不同点：冲激响应不变法幅频响应有失真 频率之间呈线性 双线性变换法幅频响应无混迭 频率之间非线性
数字Butterworth滤波器
模拟Butterworth滤波器的幅度平方函数 模拟Butterworth滤波器的幅度平方函数:\(|H_a(j\Omega)|^2=\frac{1}{1+(\Omega/\Omega_c)^{2N}}\)
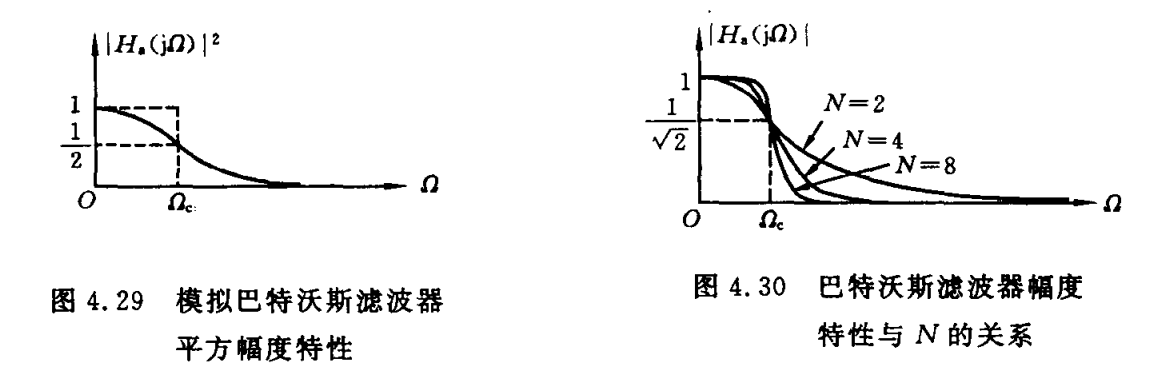特点：通带内幅度响应最平坦；通带和阻带内幅度特性单调下降；N增大，通带和阻带的近似性越好，过渡带越窄；存在极点，零点在\(\infty\) 。Butterworth滤波器极点分布特点:
令\(s=j\Omega\),则幅度平方函数为\(H_a(s)H_a(-s)=\frac{1}{1+(s/{j\Omega_c})^{2N}}\),令分母为0，则\(s_k=\Omega_ce^{j(\frac{\pi}{2N}+\frac{\pi}{2}+\frac{k\pi}{N})},k=0,1,\dots,(2N-1)\)
在s平面上共有2N个极点等角距地分布在半径为\(\Omega_c\)的圆上；极点对称于虚轴，虚轴上无极点；N为奇数，实轴上两个极点；N为偶数，实轴上无极点；各极点间的角度为\(\frac{\pi}{N}\)
根据滤波器的指标求模拟滤波器的系统函数
N为偶数时：模拟Butterworth滤波器的传递函数为 \[H_a(s)=\frac{\Omega_c^N}{\prod_{k=1}^{N/2}(s-s_k)(s-s_k^*)}\] \(s_k\)为左半平面极点，\(s_k^*\)为\(s_k\)的共轭极点，\(s_p\)为实轴上的极点 N为奇数时：\[H_a(s)=\frac{\Omega_c^N}{(s-s_p)\prod_{k=1}^{N/2-1}(s-s_k)(s-s_k^*)}\]
设计数字Butterworth滤波器的步骤
- 根据实际需要规定滤波器在数字临界频率\(w_p\)和\(w_T\)处的衰减 (单位为分贝)
- 确定模拟Butterworth滤波器的阶数N和截止频率\(\Omega_c\)
- 求模拟Butterworth滤波器的极点，并由s平面左半平面的极点构成传递函数\(H_a(s)\)
- 使用冲激不变法或双线性变换法将\(H_a(s)\)转换成数字滤波器的系统函数\(H(z)\)
IIR数字滤波器的频率变换
- 设\(H(v)\)是数字原型低通滤波器的系统函数，\(H_d(z)\)是所要求的滤波器（LP、HP、BP、BS）的系统函数。为了将稳定、因果的\(H(v)\)变换成稳定、因果的\(H_d(z)\)，要求：
- v平面到z平面的映射\(v^{-1}=F(z^{-1})\)是\(z^{-1}\)的有理函数；
- v平面的单位圆内部映射成z平面的单位圆内部。
- 频率变换的设计公式
- LP->LP:\(w_p\)要求的截止频率 \[v^{-1}=\frac{z^{-1}-\alpha}{1-\alpha z^{-1}}\qquad\alpha=\frac{sin(\frac{\theta_p-w_p}{2})}{sin(\frac{\theta_p+w_p}{2})}\]
- LP->HP:\(w_p\)要求的截止频率 \[v^{-1}=-\frac{z^{-1}+\alpha}{1+\alpha z^{-1}}\qquad\alpha=\frac{cos(\frac{\theta_p+w_p}{2})}{cos(\frac{\theta_p-w_p}{2})}\]
- LP->BP：\(w_1,w_2\)要求的上、下截止频率 \[v^{-1}=-\frac{z^{-2}-\frac{2\alpha k}{k+1}z^{-1}+\frac{k-1}{k+1}}{\frac{k-1}{k+1}z^{-2}-\frac{2\alpha k}{k+1}z^{-1}+1}\qquad\alpha=\frac{cos(\frac{w_1+w_2}{2})}{cos(\frac{w_1-w_2}{2})}\qquad k=ctg(\frac{w_2-w_1}{2})tg(\frac{\theta_p}{2})\]
- LP->BS：\(w_1,w_2\)要求的上、下截止频率 \[v^{-1}=\frac{z^{-2}-\frac{2\alpha}{k+1}z^{-1}+\frac{1-k}{k+1}}{\frac{1-k}{k+1}z^{-2}-\frac{2\alpha}{k+1}z^{-1}+1}\qquad\alpha=\frac{cos(\frac{w_1+w_2}{2})}{cos(\frac{w_1-w_2}{2})}\qquad k=tg(\frac{w_2-w_1}{2})tg(\frac{\theta_p}{2})\]
FIR数字滤波器的设计方法
基本特性: 1. FIR滤波器永远是稳定的（极点均位于原点）； 2. FIR滤波器的冲激响应\(h(n)\)是有限长序列； 3. FIR滤波器的系统函数\(H(z)\)为多项式； 4. FIR滤波器具有线性相位。 设计的基本方法： 窗函数法，频率抽样法和等波纹逼近法等。
窗函数法
窗函数法原理 将理想低通滤波器（LPF）无限长单位取样响应序列\(h_d(n)\)截断。（等效于加矩形窗），用得到的有限长序列逼近理想低通滤波器。 特点：理想低通滤波器的冲激响应序列\(h_d(n)\)无限长，非因果，不绝对可和。理想LPF是不稳定的，也是不可实现的。可以对理想LPF进行逼近：截断无限长时间冲激响应序列得到一个有限长序列。即：用有限长的冲激响应序列\(h(n)\)来逼近无限长的冲激响应序列\(h_d(n)\),\(h(n)\)应满足FIR滤波器的基本条件。应为偶对称或奇对称以满足线性相位的条件。应为因果序列。
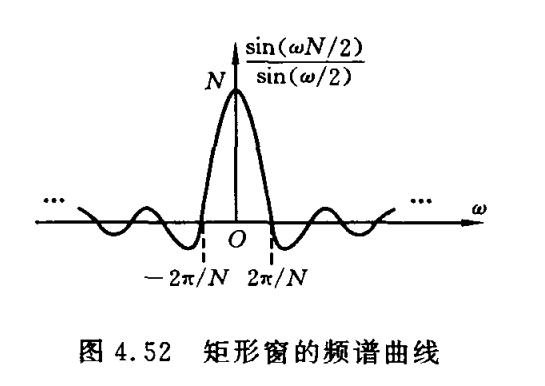
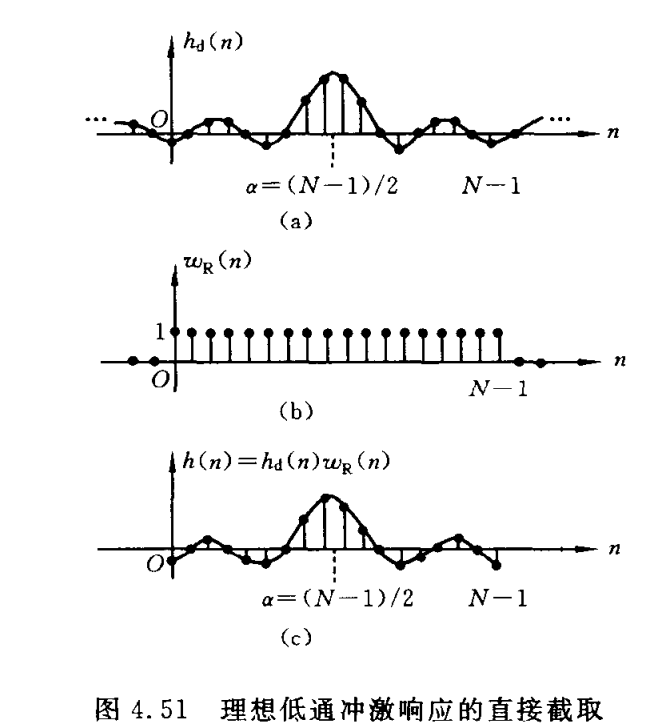其中\(w_R(n)=\begin{cases} 1,0\le n\le N-1\\ 0,else \end{cases}\)--窗函数（矩形窗），其频谱为\(H(e^{jw})=\frac{1}{2\pi}H_d(e^{jw})*W(e^{jw})\) 结论：- FIR数字滤波器的频谱是理想LPF的频谱与窗函数频谱的卷积；
- 采用不同的窗函数， \(H(e^{jw})\)就有不同的形状
由理想LPF的时间函数加窗后得到的FIR滤波器的幅度函数是理想LPF的幅度函数与窗函数幅度函数的周期卷积,其具体过程如下：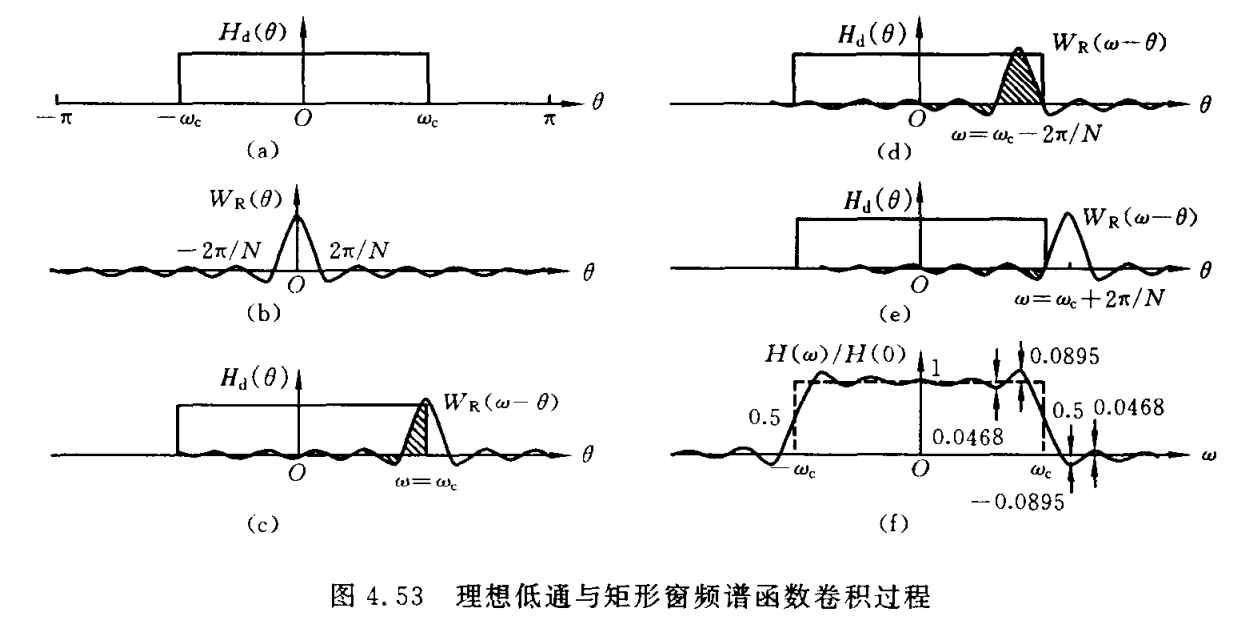 
加窗的影响 理想LPF加窗后：使滤波器的频率响应在不连续点出现了过渡带，它主要是由窗函数频谱的主瓣引起的，其宽度取决于主瓣的宽度。而主瓣的宽度\(\Delta w=\frac{4\pi}{N}\)。与滤波器的阶数N成反比。使滤波器在通带和阻带产生了一些起伏振荡的波纹—吉布斯现象，主要由旁瓣造成。
在一般情况下，对窗函数的要求是：(1)尽量减少窗函数频谱的旁瓣高度，使能量集中在主瓣，减少通带/阻带中的波纹。(2)主瓣的宽度尽量窄，获得较陡的过渡带。以上两条标准相矛盾，为了达到上述要求，采取的措施为：采用不同的窗函数。采用窗函数法设计出来的FIR数字低通滤波器的频率响应，它对理想低通滤波器的频率响应的逼近程度，取决于窗函数的频谱的主瓣宽度和旁瓣衰减的大小。
几种常用的窗函数 Bartlett窗。Hanning窗。Blackman窗。Hamming窗。Kaiser窗
窗函数的一般性质 窗函数的宽度N越大，窗函数的频谱的主瓣越窄，因而过渡带也越窄。窗函数的频谱的最大旁瓣高度和阻带最小衰减只取决于窗函数的种类，与窗函数的宽度N无关。
对窗函数的要求 为减小通带和阻带中的波纹幅度，应选择最大旁瓣高度尽可能小的窗函数，这将使更多的能量集中于主瓣内。为获得尽可能窄的过渡带，应选择主瓣宽度尽量窄的窗函数。
用窗函数法设计FIR数字滤波器的步骤
- 给出希望设计的滤波器的频率响应函数\(H_d(e^{jw})\)
- 根据允许的过渡带宽度和阻带衰减，选择窗函数和它的宽度N
- 计算希望设计的滤波器的单位取样响应\(h_d(n)\)
- 计算FIR数字滤波器的单位取样响应\(h(n)=h_d(n)w(n)\)
- 计算FIR数字滤波器的频率响应，验证是否达到所要求的指标
- 计算幅度响应和相位响应