引言
由于课程对第五章和第七章要求不高,讲述的知识点不多,所以将其整理到一起。(第七章基本没讲,故直接略过)注意:第五章前四节的知识点和随机过程讲述的知识点高度重合,故不在此赘述
5.5 相关序列和协方差序列的性质
设\(x_n,y_n\)是两个实平稳随机过程,它们的自相关序列,自协方差序列,互相关序列,互协方差序列为:\[R_{xx}(m)=E[x_nx_{n+m}]\qquad C_{xx}=E[(x_n-m_x)(x_{n+m}-m_x)]\\R_{xy}(m)=E[x_ny_{n+m}]\qquad C_{xx}=E[(x_n-m_x)(y_{n+m}-m_y)]\]
性质1:
\(C_{xx}(m)=R_{xx}(m)-m_x^2\qquad C_{xy}(m)=R_{xy}(m)-m_xm_y\\when \quad m_x=0\quad m_y=0:C_{xx}(m)=R_{xx}(m)\quad C_{xy}(m)=R_{xy}(m)\)
性质2:
\(C_{xx}(0)=\sigma_x^2\qquad R_{xx}(0)=E[x_n^2]\)
性质3:
\(R_{xx}(m)=R_{xx}(-m)\qquad C_{xx}(m)=C_{xx}(-m)\\R_{xy}(m)=R_{yx}(-m)\qquad C_{xy}(m)=C_{yx}(m)\)
性质4:
\(|R_{xy}(m)|\le (R_{xx}(0)R_{yy}(0))^{1/2}\qquad |C_{xy}(m)|\le (C_{xx}(0)C_{yy}(0))^{1/2}\\特例:|R_{xx}(m)|\le R_{xx}(0)\qquad |C_{xx}(m)|\le C_{xx}(0)\)
性质5:若\(y_n=x_{n-n_0}\),则有:\(R_{yy}(m)=R_{xx}(m)\qquad C_{yy}(m)=C_{xx}(m)\)
性质6:在随机过程中,两随机过程中时间间隔越大,它们的相关性越小\[\lim_{m \to \infty}C_{xx}(m)=0 \qquad \lim_{m \to \infty}C_{xy}(m)=0 \\ \lim_{m \to \infty}R_{xx}(m)=m_x^2 \qquad \lim_{m \to \infty}R_{xy}(m)=m_xm_y\] 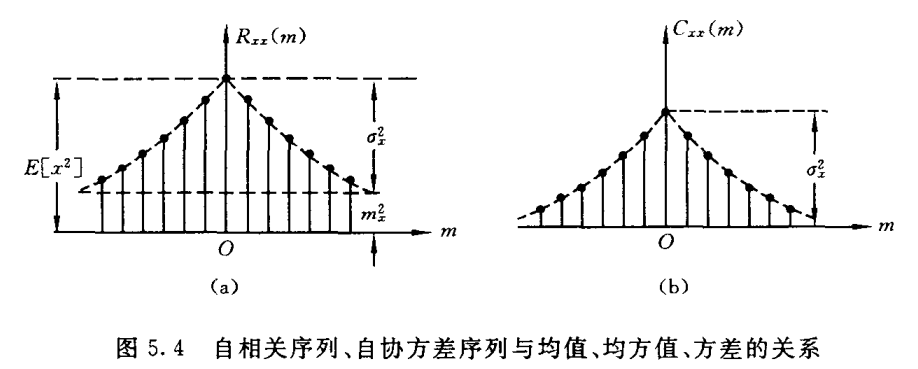
5.6 功率谱
平稳随机过程的功率谱
协方差序列的Z变换称为平稳随机过程的功率谱\(S_{xx}(z)\overset{\underset{\mathrm{\Delta}}{}}{=}\sum_{m=-\infty}^\infty C_{xx}(m)z^{-m}\)。在本课程的讨论中,功率谱总是针对于零均值随机信号,则有:\(S_{xx}(z)=\sum_{m=-\infty}^\infty R_{xx}(m)z^{-m}\),功率谱也可以表述为\(S_{xx}(e^{jw})=\sum_{m=-\infty}^\infty R_{xx}(m)e^{-jwm}\)。这两种表述都是等价的。对于一个实平稳随机过程,\(R_{xx}(m)\)的Fourier变换总是存在的,推导可得\(E[x_n^2]=\frac{1}{2\pi}\int_{-\pi}^{\pi} S_{xx}(e^{jw})\, {\rm d}w\)。功率谱在一个周期内的平均值就是随机过程的平均功率,功率谱的反变换可表述为\(R_{xx}(m)=\frac{1}{2\pi j}\oint_{C} S_{xx}(z)z^{m-1}\, \mathrm{d}z=\frac{1}{2\pi}\int_{-\pi}^{\pi} S_{xx}(e^{jw})e^{jmw}\, {\rm d}w\)
功率谱的性质
- 实平稳随机过程的功率谱是非负的
- 实平稳随机过程的功率谱是实函数
- 实平稳随机过程的功率谱是\(w\)的偶函数
平稳随机过程的互功率谱
两个平稳随机过程\({x_n}\)和\({y_n}\)的互功率谱定义为\[S_{xy}(z)=\sum_{m=-\infty}^\infty R_{xy}(m)z^{-m}\quad S_{xy}(e^{jw})=\sum_{m=-\infty}^\infty R_{xy}(m)e^{-jwm} \],由上式可得\(S_{xy}(e^{jw})=S_{yx}^*(e^{-jw})\)
5.7 离散随机信号通过线性非移变系统
整个过程可表述为: \(y(n)=\sum_{k=-\infty}^\infty h(k)x(n-k)=\sum_{k=-\infty}^\infty h(n-k)x(k)\)
其输出的均值可表述为\(m_y=m_x \sum_{k=-\infty}^\infty h(k)=m_x H(e^{j0})\)
其输出的自相关序列\(R_{yy}(m)=\sum_{k=-\infty}^\infty h(k)\sum_{r=-\infty}^\infty h(r)R_{xx}(m-r+k)\),进一步化简得\(R_{yy}(m)=R_{xx}(m)*R_{hh}(m)=R_{xx}(m)*h(m)*h(-m)\),其中:\(R_{hh}(l)=\sum_{k=-\infty}^\infty h(k)h(l+k)=h(l)*h(-l)\)为系统单位冲激响应的自相关序列
其输出的功率谱\(S_{yy}(z)=S_{xx}(z)S_{hh}(z)\),若\(h(n)\)为实序列,则\(S_{hh}(z)=H(z)H(z^{-1})\)。若\(h(n)\)为复序列,则\(S_{hh}(z)=H(z)H^*(1/z^*)\)
输入输出随机过程的互相关序列\(R_{xy}(m)=R_{xx}(m)*h(m)\),进而可以得到\(R_{yy}(m)=R_{xy}(m)*h(-m)\)
如果输入是一个零均值的平稳白噪声随机过程,其方差为\(\sigma_x^2\),自相关序列为\(R_{xx}(m)=\sigma_x^2\delta(m)\),功率谱为\(S_{xx}(z)=\sigma_x^2\),根据\(R_{yy}(m)=R_{xy}(m)*h(-m)\)有\(R_{xy}(m)=\sigma_x^2h(m)\),对其进行z变换得\(S_{xy}(z)=\sigma_x^2H(z)\)
输出随机过程的方差:\(E[y^2(n)]=R_{yy}(0)=R_{xx}(m)=\\\frac{1}{2\pi j}\oint_{C} S_{yy}(z)z^{-1}\, \mathrm{d}z=\frac{1}{2\pi j}\oint_{C} S_{xx}(z)H(z)H(z^{-1})z^{-1}\, \mathrm{d}z\) 式中的积分围线可选择为单位圆
白噪声\(w(n):m_w=0,R_{ww}=\sigma_w^2\delta(m),S_{ww}(z)=\sigma_w^2\qquad S(e^{jw})=\sigma_w^2\)