前言
因为第四章内容较少，且和第三章关系紧密，故将两章合并
导波系统的一般分析方法
导波系统的基本概念
导波（导行波）：在微波传输线中按指定方向传播的电磁波
导波系统（波导）：用来导行电磁波的装置
规则波导：沿轴线方向，横截面的形状、尺寸，以及填充介质的分布状态和电参数均不变的无限长的直波导
狭义的波导：只限于空心的金属矩形和圆形波导等。
不同类型的场
波形可划分为三类(根据纵向分量区分):
- \(\dot{E_z}=0,\dot{H_z}=0\):横电磁波：TEM波,\(\dot{\overrightarrow{E_t}}=\eta\dot{\overrightarrow{H_t}}\times\dot{\overrightarrow{a_z}}\\\dot{\overrightarrow{H_t}}=\frac{1}{\eta}\dot{\overrightarrow{a_z}}\times\dot{\overrightarrow{E_t}}\)
- \(\dot{E_z}=0,\dot{H_z}\neq 0\):横电波：TE波 H波 电场只有横向分量，纵向分量为零，所以有\(\dot{\overrightarrow{E_t}}=\frac{w\mu}{\beta}\dot{\overrightarrow{H_t}}\times\dot{\overrightarrow{a_z}}\)
- \(\dot{E_z}\neq 0,\dot{H_z}=0\):横磁波：TM波 E波 磁场只有横向分量，纵向分量为零，所以有\(\dot{\overrightarrow{H_t}}=\frac{w\epsilon}{\beta}\dot{\overrightarrow{a_z}}\times \dot{\overrightarrow{E_t}}\) TE、TM波在横截面内\(E_t\)和\(H_t\)相互正交，而且与单位矢量z构成一个右手螺旋系
波沿导波装置的传输特性
传输条件
TE波和TM波在金属波导内传输需满足一定的条件：
- \(Z(z)=A^+e^{-j\beta z}\)：无耗波导沿z轴正方向
- \(\beta=\sqrt{K^2-K_c^2}\)：相移常数
- \(K_c=\frac{2\pi}{\lambda_c}=2\pi\sqrt{\mu\epsilon}f_c\):由横截面尺寸、性质和波型决定
- \(K=w\sqrt{\mu\epsilon}\):当波导介质一定，就由该波的频率决定
- \(\beta\rightarrow f,\lambda\),当f变化时，出现以下三种情况：
- \(K>K_c,\beta\rightarrow\)实数，波导-传输状态(波向正方向和负方向传播)，此时\(\lambda<\lambda_c,f>f_c\)(\(\lambda=2\pi/(w\sqrt{\mu\epsilon})\))-工作波长，f-工作频率，与波导无关
- \(K<K_c,\beta\rightarrow\)虚数，波导-截止状态(波沿指数规律衰减)，此时\(\lambda>\lambda_c,f<f_c\)
- \(K=K_c,\beta=0\),波导-临界状态,此时\(\lambda=\lambda_c,f=f_c,f_c=\frac{K_c}{2\pi\sqrt{\mu\epsilon}},\lambda_c=\frac{2\pi}{K_c}=\frac{1}{\sqrt{\mu\epsilon}f_c}=\frac{v}{f_c},v:\)波在无界介质中传播速度，可见波导具有高通滤波器特性。(TEM波截止频率为零)
传播常数
传播常数\(\gamma=\alpha+j\beta\),衰减常数\(\alpha\):波导单位长度上波幅值的衰减量 (dB/m),相移常数\(\beta\):波沿波导轴向传播时单位距离内相位的变化量(rad/m),无耗传输线:\(\alpha=0\quad\gamma=j\beta\)
相速
相速\(v_p\): 波的等相位面沿波导轴向（z）传播的速度,\(v_p=\frac{dz}{dt}=\frac{w}{\beta}=\frac{2\pi f}{\sqrt{(\frac{2\pi}{\lambda})^2-(\frac{2\pi}{\lambda_c})^2}}=\frac{v}{\sqrt{1-(\lambda/\lambda_c)^2}}\),TEM波型的相速:\(\because \lambda_c\rightarrow\infty\quad v_p=v=\frac{1}{\sqrt{\mu\epsilon}}\),TE和TM波型相速：\(\lambda<\lambda_c,v_p>v\),可知TEM波的相速与频率无关。具有这种特性的波型称为无色散波型，对于传输某一波型的电磁波而言，其相速随频率而变化的(例如TE和TM波型)，具有这种特性的波型称为色散波型。
波导波长
波导波长\(\lambda_g\)：波导内沿轴向传播的电磁波相邻的两个同相位点之间的距离, 也就是相位相差2π的两点间的距离。\(\lambda_g=\frac{v_p}{f}=\frac{\lambda}{\sqrt{1-(\lambda/\lambda_c)^2}},\beta=\frac{2\pi}{\lambda_g}\),TEM波:\(\lambda_g=\lambda\),TE/TM波：\(\lambda<\lambda_c\quad\lambda_g>\lambda\)
群速
群速\(v_g\)：多频率成分构成的“波群”的速度（波群－－一群具有相近的ω与相近的β的波），代表能量的传播速度。\(v_g=\frac{dw}{d\beta}=v\sqrt{1-(\frac{\lambda}{\lambda_c})^2}(\lambda<\lambda_c),v_g\cdot v_p=v^2\)
波型阻抗
波型阻抗\(Z_w\)：电场的横向分量\(E_t\)与磁场的横向分量\(H_t\)的幅值之比（行波状态下）,TE波:\(Z_{TE}=\frac{w\mu}{\beta}=\sqrt{\frac{\mu}{\epsilon}}\frac{\lambda_g}{\lambda}=\eta\frac{\lambda_g}{\lambda}>\eta\),TM波:\(Z_{TM}=\frac{\beta}{w\mu}=\sqrt{\frac{\mu}{\epsilon}}\frac{\lambda}{\lambda_g}=\eta\frac{\lambda}{\lambda_g}<\eta\),TEM波：\(Z_{TEM}=\sqrt{\frac{\mu}{\epsilon}}=\eta\)(波在无界媒质中的波阻抗)\(\approx120\pi\)
矩形波导
矩形波导：通常将由金属材料制成的（一般为铜或铝，内表面镀银或金）、矩形截面的、内充空气的规则金属波导称为矩形波导。它是微波技术中最常用的传输系统之一，其优点在于微波高频段（厘米波或毫米波）损耗小、功率容量大、频带宽
场解及波型
TE波(H波)
场分量表达式：TE波型：\(E_Z=0,H_z\neq 0\),由矩形波导的边界条件:理想导体表面磁场的垂直分量\((H_x,H_y)=0\)，结合边界条件得到磁场纵向分量\(H_z=H_0cos(\frac{m\pi}{a}x)cos(\frac{n\pi}{b}y)e^{-j\beta z}\)，再进一步推导得到矩形波导其他场分量表达式，其中，最重要的是\(K_c=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}\),其与波导尺寸和传输波型有关
- 上式的m,n分别代表TE波沿x方向和y方向分布的半波个数,且每一对(m,n)对应一种波型，记为\(TE_{mn}(H_{mn})\)
- 对于TE波而言，m、n中任意一个可以为0，但是不能同时为0，故存在\(TE_{m0},TE_{0n},TE_{mn}\),矩形波导中TE波的最低次波型(截止波长最长或截止频率最低)为\(TE_{10}(a>b)\)，其余称为高次模
- 场沿z轴为行波，x,y轴为纯驻波分布，这意味着在行波状态下，沿矩形波导的纵向（z轴）传输的是有功功率，而在矩形波导的横向（x和y轴）只存在无功功率，即没有功率的传输。
场结构：为了能形象和直观的了解场的分布（场结构），可以利用电力线和磁力线来描绘它。电力线和磁力线遵循的规律：力线上某点的切线方向\(\rightarrow\)该点处场的方向,力线的疏密程度\(\rightarrow\)场的强弱,当给定了m和n时，根据场分量表达式，就可以绘出电力线和磁力线的图形----场结构图,下面举例\(TE_{10}模\)
\(TE_{10}\)波:各个场分量沿x方向有一个半驻波分布，y方向不变为均匀分布。
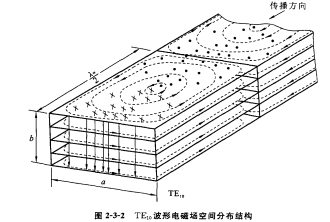
TM波（E波）
- 场分量表达式：TM波型：\(H_Z=0,E_z\neq 0\),由矩形波导的边界条件:理想导体表面切向电场为零,结合边界条件得到磁场纵向分量\(E_z=E_0sin(\frac{m\pi}{a}x)sin(\frac{n\pi}{b}y)e^{-j\beta z}\)
- 存在无穷多个波型与m、n对应，其线性组合（叠加）也是场解。每一对（m、n）对应一种波型，记为\(TM_{mn}\)。同样\(K_c=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}\)
- 对于TM波，m、n中任意一个不能为0，否则场全为0。(\(m,n=0\rightarrow E_z=0\))所以\(TM_{00}、TM_{0n}、TM_{m0}\)不存在。最低波型为\(TM_{11}\)。
- TM波型的场沿z轴为行波，沿x、y轴为纯驻波分布（正弦、余弦的分布规律）所以行波状态下，沿波导纵向（z轴）传输有功功率、横向（x、y轴）无功功率
- 场结构
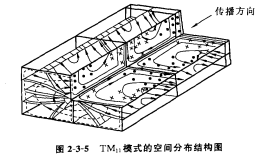
矩形波导中电磁波的传播特性
- 截止波长和截止频率 \(\lambda_c=\frac{2\pi}{K_c}=\frac{2}{\sqrt{(\frac{m}{a})^2+(\frac{n}{b})^2}},f_c=\frac{v}{\lambda_c}=\frac{1}{2\sqrt{\mu\epsilon}}\sqrt{(\frac{m}{a})^2+(\frac{n}{b})^2}\),可见\(TE_{mn},TM_{mn}\)在m、n相同时具有相同的截止波长与截止频率，但场分布不同
- 波型简并 由于矩形波导中，对于m及n均不为0的\(TE_{mn},TM_{mn}\)模，具有相同的截止波长\(\lambda_c\)，故这种场结构（波型）不同的模式截止波长相同的现象。\(TE_{0n},TE_{m0}\)是非简并模,存在简并现象的模式称为简并模，简并模在工作频率相同时，其相速、群速、波导波长都是相同的。在工作中要想办法抑制工作模的简并模。
- 截止波长分布图 因为截止波长与m,n成反比，所以当a,b一定时，m,n越小，截止波长\(\lambda_c\)越大,对应的\(\beta=\frac{2\pi}{\lambda}\sqrt{1-(\frac{\lambda}{\lambda_c})^2}\),所以当工作波长\(\lambda<\)某种模式的\(\lambda_c\)时，\(\beta>0\rightarrow\)传导模，反之则为截止模
- 主模，高次模,单模波导 截止波长最长的模式称为矩形波导中的主模其余为高次模。矩形波导中的主模为\(TE_{10}\)，其\(\lambda_c=2a\)，只能传输主模的波导为单模波导
矩形波导主模\(TE_{10}\)模场分布及工作特性
为何要单模传输？:不同模式的相速不同，他们之间将有模式色散，从而使信号发生畸变。所以微波传输系统无一例外采用单模传输，即只传输主模
\(TE_{10}\)模可以在相当宽的频带内单模工作，而在此频带内其它模式都截止。这是其得到广泛应用的主要原因
- \(TE_{10}\)模的特点:
- 只有\(E_y、H_x、H_z\)三个分量
- 各分量与y无关，即沿y轴均匀分布
- 横向场量\(E_y,H_x\)与纵向场量\(H_z\)在x方向上和z方向上相位相差π/2
- 传输特性
- \(K_c=\frac{\pi}{a}\quad\lambda_c=\frac{2\pi}{K_c}=2a\)
- \(\beta=\frac{2\pi}{\lambda}\sqrt{1-(\lambda/\lambda_c)^2}=\frac{2\pi}{\lambda}\sqrt{1-(\lambda/2a)^2}{}\\\lambda_g=\frac{2\pi}{\beta}=\frac{\lambda}{\sqrt{1-(\lambda/2a)^2}}\)
- \(v_p=\frac{w}{\beta}=\frac{v}{\sqrt{1-(\lambda/2a)^2}}\\v_g=\frac{dw}{d\beta}=v\sqrt{1-(\lambda/2a)^2}\)
- \(Z_{TE_{10}}=\frac{120\pi}{\sqrt{1-(\lambda/2a)^2}}\)
- 传输功率：\(P=\frac{abE_0^2}{480\pi}\sqrt{1-(\lambda/2a)^2}\)
- 功率容量：\(P_{br}=6\times10^5\sqrt{1-(\lambda/2a)^2}(W),a,b,\lambda\)单位均为cm
- 波导横截面尺寸选择原则
- 主要依据是单模传输：\(\lambda_{cTE_{20}}<\lambda<\lambda_cTE_{10},\lambda_{cTE_{01}}<\lambda<\lambda_cTE_{10}\\\therefore \frac{\lambda}{2}<a<\lambda,0<b<\frac{\lambda}{2}\)
- 综合考虑传输功率及损耗的要求一般对于工作于\(TE_{10}\)模的矩形波导，取\(a\approx0.7\lambda,b\approx(0.3-0.35)\lambda\)
- 管壁电流 管壁电流波在波导内传播，会在波导壁的内表面上（微米数量级）感应出的高频电流，称为管壁电流,其特点为两个侧壁的表面电流大小相等，方向相同,上下壁上的电流大小相等，方向相反
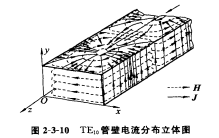该图可用于判断外部器件是否切割表面电流
圆波导
圆波导－横截面为圆形的空心金属波导管圆波导。圆波导具有加工方便、双极化、低损耗等优点，也是常用的波导管之一，可用于天线馈线、多路通信和卫星电视，可构成微波谐振腔、旋转式移相器、衰减器、旋转关节、天线辐射器等微波器件
场解及波型
圆波导的求解过程与矩形波导的求解类似，区别在于圆波导中，场量沿r方向按贝塞尔函数规律变化，沿圆周按三角函数变化。
TM波型
对于TM波型，\(H_z=0\),经过运算和贝塞尔函数性质可知，其通过边界条件可导出\(K_c=\frac{v_{mn}}{R},v_{mn}\)为m阶贝塞尔函数的第n个根的值，则可得其截止波长为\(\lambda_c=\frac{2\pi R}{v_{mn}}\)，其特点如下
- 沿圆周和半径方向均呈纯驻波分布
- \(TM_{m0}\)不存在，所以最低的波型为\(TM_{01}\)，它的\(λ_c\)最长
- m：角向波数，表示场量沿圆周分布的整驻波的个数。n：径向波数，表示场量沿半径分布的半驻波分布个数、或最大值个数
TE波型
对于TE波型，\(E_z=0\),经过运算和贝塞尔函数性质可知，其通过边界条件可导出\(K_c=\frac{\mu_{mn}}{R},\mu_{mn}\)为m阶贝塞尔函数导函数的第n个根的值，则可得其截止波长为\(\lambda_c=\frac{2\pi R}{\mu_{mn}}\)，其特点如下
- 沿圆周和半径方向均呈纯驻波分布
- \(TE_{m0}\)不存在，所以最低的波型为\(TM_{11}\)，它的\(λ_c\)最长
- m：角向波数，表示场量沿圆周分布的整驻波的个数。n：径向波数，表示场量沿半径分布的半驻波分布个数、或最大值个数
截止波长
\(\lambda_c=\frac{2\pi}{K_c}=\begin{cases} \frac{2\pi R}{v_{mn}}(TM)\\ \frac{2\pi R}{\mu_{mn}}(TE) \end{cases}\)
- 主模及高次模:圆波导中的主模为\(TE_{11},λ_c=3.41R\),其它的模均为高次模
- 简并现象
- 模式简并：\(\because J_0'(x)=-J_1(x),\therefore \mu_{0n}=v_{1n},TE_{0n},TM_{1n}\)模的\(\lambda_c\)相同
- 因为当\(m\neq 0\)时，TM波和TE波每一个模的场有两种分布可能（cos/sin），这种同一模式但具有两种极化的场分布，且\(λ_c\)相同，称为极化简并现象。
圆波导中常用的三个模式
- \(TE_{11}\):
- 是圆波导中的主模，其\(λ_c=3.41R\)
- 在横截面上，其场结构与矩形波导的\(TE_{10}\)很相似，故常用矩形波导中TE10通过方-圆接头过渡为圆波导中的\(TE_{11}\)
- 有极化简并现象，即在\(\psi\)方向场分布有\(cosm\psi\)及\(sinm\psi\)两种分布的可能,故圆波导长距离传输信号一般不用这种波型，而在旋转式移相器、衰减器、谐振腔等，常采用这种波型
- \(TE_{01}\)：
- \(TE_{01}\)也是圆波导中常用的波型之一，它的场分量只有\(E_φ,H_r,H_z,E_r＝E_z＝H_φ＝0\)
- 为圆波导中的高次模， \(λ_c=1.64R\)
- m=0，场结构在横截面上是轴对称的（与\(\psi\)无关），所以无极化简并。但是与\(TM_{11}\)存在模式简并，又称为E－H简并。故在使用时必须设法抑制低次模及简并模。
- 该波型在波导内壁的切向磁场只有\(H_z\)分量，故内壁上只有圆周方向的(\(\psi\)方向)的表面电流，导体损耗小
- 当传输功率一定时，频率越高，则损耗越小。所以该模式适合作为高Q谐振腔的工作模式，以及用来长距离传输功率信号
- \(TM_{01}\)：
- \(TM_{01}\)场分量只有\(H_φ,E_r,E_z,H_r＝H_z＝E_φ＝0\)
- 是横磁模中的最低模式,\(λ_c=2.61R\)
- 横截面上的场结构具有轴对称性，即沿\(\psi\)向无变化,故无极化简并，也无模式简并，因此常作为雷达天线与馈线的旋转关节中的工作模式。
- 该波型在内壁表面的切向磁场只有\(H_\psi\)分量，只有z方向的管壁电流，因此它可以有效地和轴向流动的电子流交换能量，由此将其应用于微波电子管中的谐振腔及直线电子加速器中的工作模式
同轴线
同轴线的优点：主波型（主模）是TEM波，是无色散波，无频率下限、频带宽，场结构稳定，比双绞线损耗小。
同轴线的缺点：随着频率升高，功率容量下降，导体与介质损耗增加。所以一般只能用于分米波和厘米波的低频段
TEM波的传输特性
- \(K_c=0\Rightarrow\lambda_c=\infty,\beta=K=w\sqrt{\mu\epsilon},\lambda_g=\lambda\\v_p=v_g=v=\frac{1}{\sqrt{\mu\epsilon}},Z_{TEM}=\eta=\sqrt{\frac{\mu}{\epsilon}}\)
- 特性阻抗:\(Z_0=\frac{\eta}{2\pi}ln\frac{b}{a}=\frac{60}{\sqrt{\epsilon_r}ln\frac{b}{a}}\)
- 传输功率:\(P_{br}=\sqrt{\epsilon_r}\frac{a^2E_0^2}{120}ln\frac{b}{a}(w)\)
高次模及横向尺寸的选择
当工作波长减少到与同轴线的横向尺寸可以相比拟时，同轴线中会出现高次模,一般不用高次波型传输功率，而采用主模TEM来传输功率。为了做到单模传输，就需要抑制高次模。
同轴线中最低的高次模为\(TE_{11}\)，截止波长\(λc\approx\pi(b+a)\)所以得到横向尺寸选择的依据
- 保证主模单模工作:\(\lambda_{min}>\lambda_cTE_{11}=\pi(b+a),\therefore a+b<\frac{\lambda_{min}}{\pi}\)
- 使传输功率容量最大
微带传输线
上一章介绍了规则金属波导传输系统的传输原理及特性, 这类传输系统具有损耗小、结构牢固、功率容量高及电磁波限定在导管内等优点, 其缺点是比较笨重、高频下批量成本高、 频带较窄等。随着航空、航天以及通信发展的需要, 对微波设备提出了体积要小、重量要轻、 可靠性要高、性能要优越、一致性要好、 成本要低等要求, 这就促成了微波技术与半导体器件及集成电路的结合, 产生了微波集成电路。对微波集成传输元件的基本要求之一就是它必须具有平面型结构, 这样可以通过调整单一平面尺寸来控制其传输特性, 从而实现微波电路的集成化。微带线就是一种微波集成电路中应用最广泛的平面传输线。
微带线
微带传输线的基本结构有两种形式: 带状线和微带线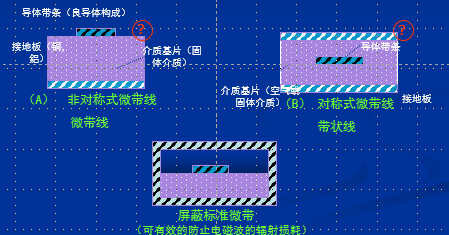 
带状线由同轴线演化而来，其流程如下，主要传输的还是TEM波 
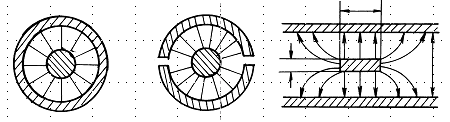微带线是由沉积在介质基片上的金属导体带和接地板构成的一个特殊传输系统, 它可以看成由双导体传输线演化而来 
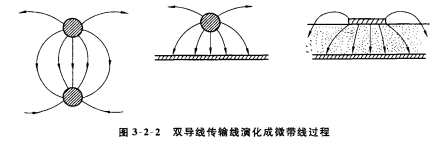由于这种开放式不对称结构导致微带线是一种不均匀介质填充的传输线，可以证明微带中的电磁场必有纵向分量，即在微带线中不能导行TEM波，但是在工作频率较低时，由于微带线基片厚度h远小于微带波长，其纵向分量很小，可以忽略，此时的场结构与TEM模相似，此时的传输波型为准TEM模。它是微带线的主模。
微带线的特性阻抗
如果微带线是由\(\epsilon_r\)的均匀介质包围，则\(Z_0^0=\sqrt{\frac{L}{C}}=\frac{1}{v_pC},v_p=\frac{1}{\sqrt{LC}}=\frac{v_0}{\sqrt{\epsilon_r}},\lambda=\frac{v_p}{f}=\frac{\lambda_0}{\sqrt{\epsilon_r}}\)
但是微带线实际上是介质与空气的混合介质系统,所以引入等效相对介电常数的概念: \(C_0\)--单一空气介质包围的微带线的分布电容,\(C_1\)--实际空气+介质填充微带线的分布电容，等效相对介电常数\(\epsilon_{re}=\frac{C_1}{C_0}\)
即把实际混合介质系统想象成单一的、均匀的相对介电常数\(ε_{re}\)的介质构成的系统,所以\(Z_0=\frac{Z_0^0}{\sqrt{\epsilon_{re}}}\quad Z_0^0=\frac{1}{v_pC_0},Z_0^0\)为同样形状尺寸下填充介质全部是空气的微带线的特性阻抗
两组实用的工程计算公式
- 假设导体带厚度为零：\(\epsilon_{re}\approx \frac{\epsilon_r+1}{2}+\frac{\epsilon_r-1}{2}(1+\frac{10h}{W})^{-1/2}=1+q(\epsilon_r-1),q=\frac{1}{2}[1+(1+\frac{10h}{W})^{-1/2}]:\)填充系数，表示\(\epsilon_r>1\)的介质填充程度
- 导体带厚度不为零时，这时的解法一般是把边缘电容增加的影响等效为导体带的宽度增加了△ω，即此时的导带宽度为\(W_e=w+\Delta w,\Delta w\)的工程近似计算公式为 \[\frac{w}{h}\le\frac{1}{2\pi}:\Delta w=\frac{t}{\pi}(ln\frac{4\pi w}{t}+1)\\\frac{w}{h}\ge\frac{1}{2\pi}:\Delta w=\frac{t}{\pi}(ln\frac{2h}{t}+1)\]
其他参量：相速度\(v_p=\frac{v_0}{\sqrt{\epsilon_{re}}}\quad\lambda_g=\frac{\lambda_0}{\sqrt{\epsilon_{re}}}\leftrightarrow\beta=k_0\sqrt{\epsilon_{re}}\)