前言
因为第六章内容较少，故将两章合并
概述
- 为什么在微波波段不能使用集总参数LC谐振回路？
- \(w_0=1/\sqrt{LC}\)在微波波段，\(w_0\)很高，所以L和C很小，元件制造困难
- 当电路尺寸与微波波长可以相比拟时，就会产生能量的辐射，波长越短辐射越严重，故辐射损耗大。另外，由于此时趋肤效应严重，故欧姆损耗大，而且介质损耗大。因此，在频率较高的微波波段，集总LC谐振回路储能小，损耗大，导致Q值小到不能用
- 微波谐振器与LC谐振回路的相同和相异点
- LC回路为集总参数电路，微波谐振器时属于分布参数电路。所以LC回路能量只分布在L、C上，而微波谐振器的能量分布在整个腔体中
- LC回路在L及C一定时，只有一个谐振频率，而微波谐振器有无限多个谐振频率，这称为微波谐振器的多谐性
- 微波谐振腔储能多，损耗小。故微波谐振器品质因数很高，比LC回路的Q值高很多。
- 微波谐振器的分析方法：主要是场解法和场的叠加法，这里主要用的是后者
微波谐振器的主要参数
- 谐振频率：无色散波\(\beta=\frac{2\pi}{\lambda_r}=\frac{2\pi}{v}f\),色散波\(\beta=\frac{2\pi}{\lambda_g}=\frac{2\pi}{v}\sqrt{f_r^2-f_c^2}\)
- 品质因数
- 固有品质因数:表征谐振器的损耗的大小、频率选择性的强弱、工作稳定度 \[Q_0=2\pi\frac{W(腔体总储能)}{W_T(腔体一个周期损耗能量)=PT(P:一周期谐振器平均损耗功率)}\\\therefore Q_0=\frac{2\pi W}{PT}=w_r\frac{W}{P}\] 进一步化简可知\(Q_0\)正比于\(V/S\),其与谐振器尺寸成正比，又因谐振器尺寸与工作波长成正比，所以其与工作波长成正比
- 有载品质因数：谐振器带上负载时腔体的品质因数 \[Q_L=w_r\frac{W}{P_i+P_c}或\frac{1}{Q_L}=\frac{1}{Q_0}+\frac{1}{Q_c}或Q_L=\frac{Q_0}{1+k}\] \(W-总储能，P_i-腔本身损耗功率，P_c-外界负载损耗功率，\\Q_c-耦合品质因数，k-耦合系数(腔体与外界负载之间的耦合程度)\)
圆柱谐振腔
圆柱谐振腔具有较高的品质因数，调谐方便，结构坚固，易于加工，制作。属于传输线型谐振腔，可以看作两端短路的一段圆波导
场分量表达式
- \(TE_{mnp}\)振荡模式：先根据边界条件求出\(H_z\)，其形式与圆波导有一定相似性，其在\(r,\psi,z\)上均呈驻波状态，相位常数\(\beta=\frac{p\pi}{l}\),再进而利用场分量间的关系可以进一步求出其他分量，其中\(K=\sqrt{(\frac{\mu_{mn}}{R})^2+(\frac{p\pi}{l})^2},m=0,1,2,\dots,n=1,2\dots,p=1,2\dots\)
- \(TM_{mnp}\)振荡模式：先根据边界条件求出\(E_z\)，其形式与圆波导有一定相似性，其在\(r,\psi,z\)上均呈驻波状态，相位常数\(\beta=\frac{p\pi}{l}\),再进而利用场分量间的关系可以进一步求出其他分量，其中\(K=\sqrt{(\frac{v_{mn}}{R})^2+(\frac{p\pi}{l})^2},m=0,1,2,\dots,n=1,2\dots,p=0,1,2\dots\)
谐振频率和波型图
- 谐振频率： \(f_r=\frac{Kv}{2\pi}\Rightarrow\lambda_r=\frac{v}{f_r}=\frac{2\pi}{K},\therefore TE_{mnp}:f_r=\frac{1}{2\pi\sqrt{\mu\epsilon}}\sqrt{(\frac{\mu_{mn}}{R})^2+(\frac{p\pi}{l})^2},\lambda_r=\frac{1}{\sqrt{(\frac{\mu_{mn}}{2\pi R})^2+(\frac{p}{2l})^2}},\\\therefore TM_{mnp}:f_r=\frac{1}{2\pi\sqrt{\mu\epsilon}}\sqrt{(\frac{v_{mn}}{R})^2+(\frac{p\pi}{l})^2},\lambda_r=\frac{1}{\sqrt{(\frac{v_{mn}}{2\pi R})^2+(\frac{p}{2l})^2}}\)
- 波形图：如果用\(X_{mn}\)来代替上式中的\(\mu_{mn}\)和\(v_{mn}\)，则圆柱谐振腔中的 谐振波长\(\lambda_r\)可以写成一个公式\(\lambda_r=\frac{1}{\sqrt{(\frac{X_{mn}}{2\pi R})^2+(\frac{p}{2l})^2}}=\frac{D}{\sqrt{(\frac{X_{mn}}{\pi})^2+(\frac{Dp}{2l})^2}}\rightarrow(f_rD)^2=(\frac{vX_{mn}}{\pi})^2+(\frac{vp}{2})^2(\frac{D}{l})^2\),从上面关系式可知，对于给定模式，\((f_rD)^2与(\frac{D}{l})^2\)在波形图上是一直线,斜率为\((\frac{vp}{2})^2\),截距为\((\frac{vX_{mn}}{\pi})^2\)
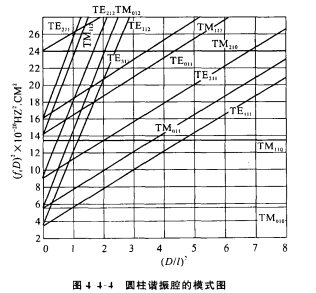工作方块：以选定工作波型的调谐曲线为对角线，最小、最大的\((f_rD)^2\)值与对应的 \((D/l)^2\)确定的矩形区域。利用工作方块保证单模工作，避免干扰波型：
- 自干扰型：相同m、n，不同p-相同截距，不同斜率，与工作波型耦合最强，务必不使其落入工作方块内
- 一般干扰型：相同p，不同m、n-不同截距，相同斜率，会导致一个以上的谐振频率。
- 交叉型：m、n、p完全不同-场结构完全不同。
- 简并型：曲线完全重合，fr完全相同，但场结构完全不同，容易抑制。
- 圆柱谐振腔特点：
- 圆柱腔存在多谐性
- R、l一定时，谐振波长\(λ_r\)最长的模为主模。当l>2.1R时，\(TE_{111}\)为主模,当l<2.1R时，\(TM_{010}\)为主模
- \(TE_{onp}\)与\(TM_{1np}\)模式简并，同时都存在极化简并
- 圆柱腔常用的3个振荡模式
- \(TE_{011},K_c=\frac{3.832}{R},\lambda_r=1/\sqrt{(\frac{1}{1.64R})^2+(\frac{1}{2l})^2}\)为高次模，磁场分量只有\(H_r,H_\psi\),侧壁和端壁内表面只有\(\psi\)方向表面电流，可用不接触式活塞进行调谐，场结构稳定、无极化简并，损耗小，Q值可高达几万以上。故可作成高精度的频率计
- \(TE_{111},\lambda_r=1/\sqrt{(\frac{1}{3.41R})^2+(\frac{1}{2l})^2},l>2.1R\)时，为圆柱谐振腔的主模，腔体尺寸较小，Q值不高，存在极化简并
- \(TM_{010},K_c=\frac{2.405}{R},\lambda_r=2.61R,l<2.1R\)为主模,既无模式简并，又无极化简并.Q值不高，且\(λ_r\)与l无关，故无法用短路活塞来进行调谐,常用的调谐方法从端面中心插入一圆柱体，插入深度可调
矩形谐振腔
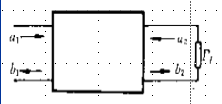
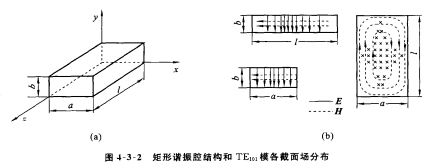
矩形空腔谐振器是由一段长为l、 两端短路的矩形波导组成
场解及振荡模式
- \(TE_{mnp}\)振荡模式：先根据边界条件求出\(H_z\)，其形式与矩形波导有一定相似性，相位常数\(\beta=\frac{p\pi}{l}\),再进而利用场分量间的关系可以进一步求出其他分量，其中\(K=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2+(\frac{p\pi}{l})^2},m,n不同时为0,p=1,2\dots\)
- \(TM_{mnp}\)振荡模式：先根据边界条件求出\(E_z\)，其形式与矩形波导有一定相似性，相位常数\(\beta=\frac{p\pi}{l}\),再进而利用场分量间的关系可以进一步求出其他分量，其中\(K=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2+(\frac{p\pi}{l})^2},m,n\neq0,p=1,2\dots\)
特性参数
- 谐振频率、谐振波长 \(f_r=\frac{Kv}{2\pi}\Rightarrow\lambda_r=\frac{v}{f_r}=\frac{2\pi}{K},\therefore f_r=\frac{1}{2\sqrt{\mu\epsilon}}\sqrt{(\frac{m}{a})^2+(\frac{n}{b})^2+(\frac{p}{l})^2},\lambda_r=\frac{2}{\sqrt{(\frac{m}{a})^2+(\frac{n}{b})^2+(\frac{p}{l})^2}}\)
- 固有品质因数(以\(TE_{101}\)为例) \[Q_0=\frac{abl}{\delta}\frac{a^2+l^2}{2b(a^3+l^3)+al(a^2+l^2)}\]
同轴线空腔谐振器
同轴腔由一段长为l的同轴线构成，其振荡模式为TEM模。优点：场结构简单、稳定，无色散，无频率下限，工作频带宽 ,缺点：固有品质因数Q值比较低，损耗大，故工作频率不能太高,适用：米波、分米波、厘米波（小功率）低精度的波长计,主要可分为\(\lambda/2\)同轴腔：\(\lambda_r=\frac{2l}{p}\)和\(\lambda/4\)同轴腔:\(\lambda_r=\frac{4l}{2p+1}\)与电容加载同轴谐振腔\(l<(2p+1)\frac{\lambda_r}{4}\)
微波网络基础
微波网络模型由一个通常称之为“黑箱”的N与外部相连接的若干端口构成。 “黑箱”表示不均匀性，端口是它与外界相联系的“窗口”，电信号由端口输入或输出，并可在端口处进行电压、电流、反射系数和衰减等量的测量。其优点在于不用关心黑盒内部长的具体实现情况，只需要通过测量的方式知道各端口信号量之间的关系，避免了对内部场分布的复杂计算
微波网络与传输矩阵
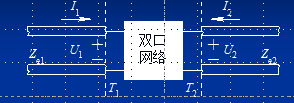线性微波网络（Network），输入电压电流\(U_1、I_1\)和输出电压电流\(U_2、I_2\)可用传输矩阵[A]联系起来 \[\begin{bmatrix}
U_1\\
I_1\\
\end{bmatrix}=\begin{bmatrix}
A_{11}&A_{12}\\
A_{21}&A_{22}\\
\end{bmatrix}\begin{bmatrix}
U_2\\
-I_2\\
\end{bmatrix}=A\begin{bmatrix}
U_2\\
-I_2\\
\end{bmatrix}\] A称为二端口网络的传输矩阵，其元素\(A_{11}、A_{12}、A_{21}和A_{22}\)称为传输参数（A参数）,A参数的定义式可以在端口开路和短路的情况下求得，A参数各参数的物理意义为： \(A_{11}\)：端口②开路时，端口①到端口②电压传输系数的倒数； \(A_{21}\)：端口②开路时，端口①与端口②之间的转移导纳； \(A_{21}\)：端口②短路时，端口①到端口②电流传输系数的倒数； \(A_{22}\)：端口②短路时，端口①与端口②之间的转移阻抗。
由于A参数是在网络端口开路和短路的情况下求出的，因此称为混合A参数，并具有明确的物理意义。互易网络:\(A_{11}A_{22}-A_{12}A_{21}=1\)对称网络:\(A_{11}=A_{22}\)
微波网络的散射参数
\[\begin{bmatrix} b_1\\ b_2\\ \end{bmatrix}=\begin{bmatrix} S_{11}&S_{12}\\ S_{21}&S_{22}\\ \end{bmatrix}\begin{bmatrix} a_1\\ a_2\\ \end{bmatrix}\] 简记为b=Sa,b和a分别为由端口的归一化反射波和归一化入射波所构成的列矩阵，S是一个正方矩阵,称为二端口网络的归一化散射矩阵，其元素称为归一化的散射参数，也称为S参数
S参量各参数的物理意义为： \(S_{11}\)：端口②接匹配负载时，端口①的反射系数； \(S_{21}\)：端口②接匹配负载时，端口①到端口②波的传输系数； \(S_{22}\)：端口①接匹配负载时，端口②的反射系数； \(S_{12}\)：端口①接匹配负载时，端口②到端口①波的传输系数。 可见, ［S］矩阵的各参数是建立在端口接匹配负载基础上的反射系数或传输系数。 这样利用网络输入输出端口的参考面上接匹配负载即可测得散射矩阵的各个参量。 对于互易网络: \(S_{12}=S_{21}\) 对于对称网络: \(S_{11}=S_{22}\)
二端口网络的工作特性参量
二端口元件是微波系统中用的最多的元件,将这些二端口元件接入到传输系统后，相当于在均匀传输线中插入一个二端口网络,此时其输入端的反射系数不仅与网络参量有关，而且还与输出端所接的负载有关 