前言
第一章内容较少，故将一二章合并。本知识小结只针对华中科技大学电子信息与通信学院课程《通信电子线路》进行总结，不保证满足所有读者需求
通信系统导论
通信系统组成框图如下 
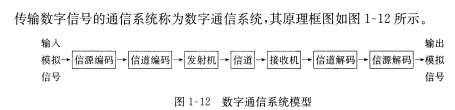
超外差接收机框图：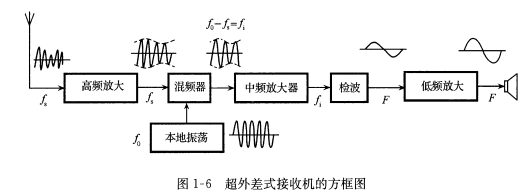 
通信电子线路分析基础
选频网络
选频网络的作用是选出我们需要的频率分量并滤除不需要的频率分量。选频网络可分 为谐振回路和滤波器两大类
谐振回路 由电感和电容元件组成的振荡回路，振荡回路包含单振荡回路和耦合振荡回路，而单振荡回路又包含串联谐振回路和并联谐振回路。 滤波器滤波器包含LC集中滤波器 、石英晶体滤波器 、陶瓷滤波器和声表面波滤波器 等 。 滤波器的优点是稳定性好，电性能好，品质因数高，利于微型化，便于大量生产
串联谐振回路
电感电容信号源三者串联称为串联回路，其在谐振频率或谐振频率附近工作时，称为串联谐振回路，下面将归纳串联谐振回路的参量进行分析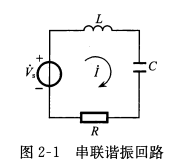 
回路阻抗 设z为回路阻抗，则回路阻抗可表述为\(z=R+j(wL-\frac{1}{wC})\),进一步化简即可的其阻抗模与阻抗幅角为\(|z|=\sqrt{R^2+(wL-\frac{1}{wC})^2},\psi_z=arctan\frac{wL-\frac{1}{wC}}{R}\)
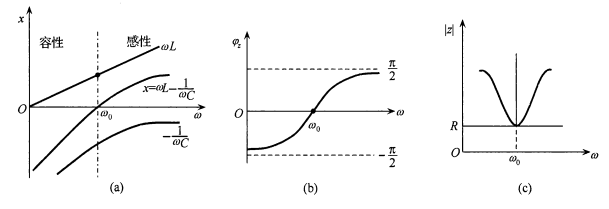又上图可知，当\(w>w_0\)时，回路成感性，电流滞后电压，反之则成容性，电流超前电压，\(w=w_0，|z|=R\)，回路串联谐振，当回路谐振时的感抗或容抗,称为特性阻抗，用\(\rho\)表示，\(\rho=w_0L=\frac{1}{w_0C}=\sqrt{\frac{L}{C}}\)谐振频率\(f_0\) 由上一小节的推导知，串联谐振回路的谐振频率就是当\(wL-\frac{1}{wC}=0\)的信号频率\(w_0=\frac{1}{\sqrt{LC}},f_0=\frac{1}{2\pi\sqrt{LC}}\)
品质因数Q 谐振时回路感抗值(或容抗值)与回路电阻R 的比值称为回路的品质因数，以Q表示,表示回路损耗大小 \[Q=\frac{w_0L}{R}=\frac{1}{w_0CR}=\frac{\rho}{R}=\frac{1}{R}\cdot\sqrt{\frac{L}{C}}\] 且在串联谐振时，电感L和电容C上的电压达到最大值且为输入信号电压的Q倍,故串联谐振也称为电压谐振。因此，必须预先注意回路元件的耐压问题
广义失谐系数\(\xi\) 广义失谐是表示回路失谐大小的量，谐振时为0 \[\xi=\frac{失谐时电抗}{谐振时电阻}=\frac{X}{R}=Q_0(\frac{w}{w_0}-\frac{w_0}{w}),when\quad w\approx w_0,\xi\approx Q_0\cdot\frac{2\Delta f}{f_0}\]
谐振曲线 串联谐振回路中电流幅值与外加电动势频率之间的关系曲线称为谐振曲线,可用\(N(f)\)表示谐振曲线函数, \[N(f)=\frac{失谐处电流}{谐振点电流}=\frac{1}{1+j\xi}\] Q 值不同即损耗R 不同时，对曲线有很大的影响,Q值大，曲线尖锐，选择性好 ;Q小 ，曲线钝,通带宽
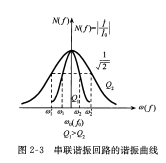
通频带 当回路外加电压的幅值不变时，改变频率，回路电流下降到\(\frac{1}{\sqrt{2}}\)时所对应的频率范围称为谐振回路的通频带，用B表示 \[B=2\Delta f_{0.7}=\frac{f_0}{Q}\] 所以B与Q成反比,Q增大,B减小,B的推导用到了广义失谐函数辅助推导，在这里省略
相频特性曲线 其用于表示回路电流相角\(\psi_i\)随频率w变化的曲线,\(\psi_i=-arctan\frac{x}{R}=-arctan\xi\)
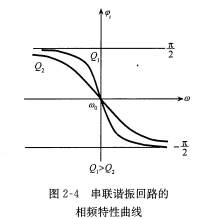
信号源内阻及负载对串联谐振回路的影响 若考虑信号内阻\(R_s\)与负载\(R_L\)，则有载Q值可表述为\(Q_L=\frac{w_0L}{R+R_s+R_L}\),可以看出串联谐振回路适合\(R_s\)很小和\(R_L\)不大的电路，这样\(Q_L\)不会太低，有较好的选择性
并联谐振回路
由电感、电容、信号源三者并联组成的回路称为并联谐振回路，其中\(R_p=\frac{L}{RC}\)，是把电感的R转换到独立支路上得到的等效电阻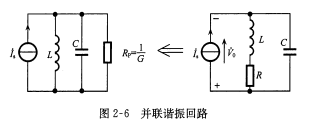 
- 回路阻抗 对于并联回路来说，一般采用导纳分析比较方便，其导纳 \[Y=\frac{1}{z}=\frac{CR}{L}+j(wc-\frac{1}{wL})=G+jB\]
- 谐振频率 与串联谐振回路一致为：\(w_p=\frac{1}{\sqrt{LC}},f_p=\frac{1}{2\pi\sqrt{LC}}\)，其阻抗特性如下，\(w>w_p\),回路呈容性，反之为感性
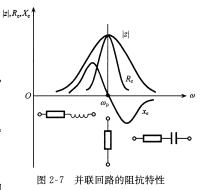
- 品质因数 与串联谐振回路类似为 \[Q_p=\frac{w_pL}{R}=\frac{R_p}{w_pL}=\frac{R_p}{\rho}=R_p\cdot\sqrt{\frac{C}{L}}\] 式中,R为串联在电感支路的损耗电阻;\(R_P\)为并联谐振回路的谐振电阻,且在并联谐振时，电感L和电容C上的电流达到最大值且为输入信号电流的Q倍,故串联谐振也称为电流谐振。
- 广义失谐系数\(\xi\) 广义失谐是表示回路失谐大小的量，谐振时为0 \[\xi=\frac{失谐时电纳}{谐振时电导}=\frac{B}{G}=\frac{w_pC}{G}(\frac{w}{w_p}-\frac{w_p}{w}),when\quad w\approx w_p,\xi\approx Q_p\cdot\frac{2\Delta f}{f_p}\]
- 谐振曲线 并联谐振回路中电压幅值与外加电动势频率之间的关系曲线称为谐振曲线,可用\(N(f)\)表示谐振曲线函数, \[N(f)=\frac{失谐处电压}{谐振点电压}=\frac{1}{1+j\xi}\] Q 值不同时，对曲线有很大的影响,Q值大，曲线尖锐，选择性好 ;Q值小，曲线钝,通带宽
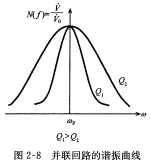
- 通频带 当回路外加电流的幅值不变时，改变频率，回路电压下降到\(\frac{1}{\sqrt{2}}\)时所对应的频率范围称为谐振回路的通频带，用B表示 \[B=2\Delta f_{0.7}=\frac{f_p}{Q_p}\] 所以B与Q成反比,Q增大,B减小,B的推导用到了广义失谐函数辅助推导，在这里省略
- 相频特性曲线 其用于表示回路电压相角\(\psi_v\)随频率w变化的曲线,\(\psi_v\approx-arctan\xi\)
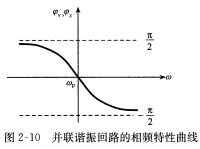
- 信号源内阻及负载对串联谐振回路的影响 若考虑信号内阻\(R_s\)与负载\(R_L\)，则有载Q值可表述为\(Q_L=\frac{Q_p}{1+\frac{R_p}{R_s}+\frac{R_p}{R_L}}\),可以看出并联谐振回路适合\(R_s\)很大和\(R_L\)很大的电路，这样\(Q_L\)不会太低，有较好的选择性，适用于恒流源。
串并联阻抗等效互换与回路抽头阻抗互换
串并阻抗的等效互换
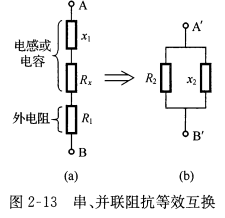在实际电路中有时为了分析电路方便需进行串、并联电路的等效互换，若\(Z_{AB}=Z_{A'B'}\),则经过推导可得 \[R_2=(1+Q_L^2)(R_1+R_x),x_2=x_1(1+\frac{1}{Q_{L}^2})\\when\quad Q_L>>1,R_2\approx(R_1+R_2)Q_L^2,x_2\approx x_1\]
回路抽头时阻抗的变化（折合）关系
从前面分析可知,\(R_s,R_L\)对回路Q值有影响，实际应用中为了减小信号源内阻和负载对回路的影响。采用抽头接入方式如下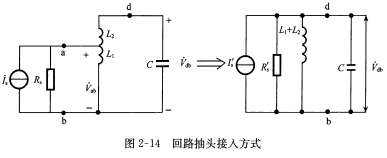 
其接入系数P定义为抽头点电压与端电压之比，利用能量等效原则有如下关系 \[P=\frac{L_1}{L_1+L_2}=\frac{N_1}{N_1+N_2}\] 若为电容抽头，则有 \[P=\frac{C}{C_2}=\frac{C_1}{C_1+C_2}\] 
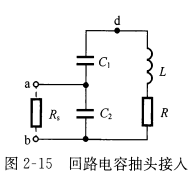根据以上分析得出结论: 1. 抽头改变时，接入系数p改变 2. 由低抽头折合到回路高端，等效导纳降低为原来的\(P^2\),等效电阻提升\(\frac{1}{P^2}\),Q提升很多 3. 对电流源来说与阻抗导纳的区别是低抽头向高抽头转换，电流源减小为原来的P，电压源减小为原来的\(\frac{1}{P}\) 4. 负载电容的折合则是等于原来的\(P^2\)，折合后电容减小，阻抗加大
插入损耗：\(K=\frac{无损输出功率P_1}{有损输出功率P_1'}=(\frac{1}{1-\frac{Q_L}{Q_0}})^2\)
耦合回路
耦合回路的形式
耦合回路是由相互间有影响的两个回路组成的，其中接入信号源的回路称为初级回路,与它相互耦合的第二个回路连接负载，称 为次级回路。如果初、次级回路都是谐振回路，则称为耦合振荡回路。耦合振荡回路可以改善谐振曲线,使其选频特性更接近理想的矩形曲线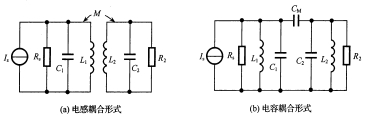 
为了说明回路间耦合程度的强弱，引入耦合系数的概念并以k表示，对于电感耦合回路有\(k=\frac{C_M}{\sqrt{C_1+C_M}\sqrt{C_2+C_M}}\),对于电感耦合回路\(k=\frac{M}{\sqrt{L_1L_2}}\)
反射阻抗与耦合回路的等效阻抗
一般来说我们更关心的是反射阻抗与耦合回路的等效阻抗，其中反射阻抗用来说明一个回路对另一回路电流的影响，对初次级回路的相互影响，可以用一个反射阻抗来表示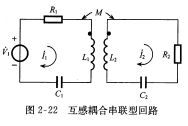 
根据上图进行推导，可以求出次级回路对初级回路的反射阻抗\(Z_{f1}=\frac{(wM)^2}{Z_{22}}\),初级回路对次级回路的反射阻抗\(Z_{f2}=\frac{(wM)^2}{Z_{11}}\),经过上述分析可得到等效电路如下 
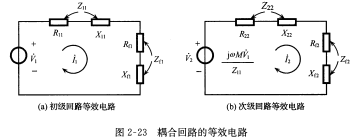将自阻抗分解为电阻分量和电抗分量后可得 \[Z_{f1}=\frac{(wM)^2}{R_{22}^2+X_{22}^2}R_{22}+-j\frac{(wM)^2}{R_{22}^2+X_{22}^2}X_{22}\\Z_{f2}=\frac{(wM)^2}{R_{11}^2+X_{11}^2}R_{22}+-j\frac{(wM)^2}{R_{11}^2+X_{11}^2}X_{11}\] 由上式可知：反射电阻永远是正值。这是因为，无论是初级回路反射到次级回路，还是从次级回路反射到初级回路，反射电阻总是代表一定能量的损耗；反射电抗的性质与原回路总电抗的性质总是相反的；反射电阻和反射电抗的值与耦合阻抗的平方值\((wM)^2\)成正比
耦合回路的调谐
对于耦合谐振回路，凡是达到了初级等效电路的电抗为零，或次级等效电路的电抗为零或初、次级回路的电抗同时为零，都称为回路达到了谐振，根据调谐参数不同，可分为部分谐振、复谐振和全谐振三种情况
- 部分谐振：如果固定次级回路参数与耦合量不变，调节初级回路的电抗使初级回路达到电抗和为0，称初级回路达到部分谐振，也可调节次级回路电抗使初级回路达到部分谐振
- 复谐振：在部分谐振的条件下，再改变互感量使得反射电阻等于回路本身电阻，即满足最大功率传输条件，使次级回路电流达到最大值，称为复谐振，此时单独对两个回路来看都失谐，但是他们的等效回路都对信号源频率谐振
- 全谐振：调节初级回路的电抗及次级回路的电抗,使两个回路都单独地达到与信号源频率谐振(电抗为0)，即耦合回路达到全谐振，如果进一步改变M使得\(R_{11}=R_{f1},R_{22}=R_{f2}\),则称为最近全谐振，此时有\(M_c=\frac{\sqrt{R_{11}R_{22}}}{w},k_c\approx\frac{1}{\sqrt{Q_1Q_2}}\):临界耦合系数，且注意耦合回路的通频带\(B=\sqrt{2}\frac{f_0}{Q}\)
石英谐振器
石英晶体的特点如下：等效电感特别大，等效电容特别小，所以Q值很大；外电路影响很小。
电路有两个谐振角频率，串联谐振角频率和并联谐振角频率，其中，串联谐振频率\(w_q=\frac{1}{L_qC_q}\),并联谐振频率\(w_p=\frac{1}{\sqrt{L_q\frac{C_0C_q}{C_0+C_q}}}\)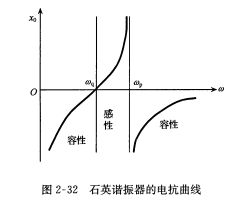 
由石英谐振器设计出来的石英晶体滤波器的电抗曲线如下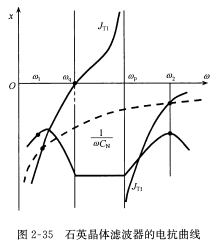 
非线性电路分析基础
非线性元件的参数与通过它的电流或施加于其上的电压有关，非线性元件构成的电路就是非线性电路
非线性电路中至少包含一个非线性元件，其输出输入关系用非线性函数或微分方程表达，不具备叠加型和均匀性，是其与线性电路的主要区别
非线性电路的输入输出关系是非线性函数关系，当信号通过非线性电路后，在输出 信号中将会产生输入信号所没有的频率成分,也可能不再出现输入信号中的某些频率成分。 这是非线性电路的重要特性
非线性电路的分析方法主要有以下三种：
- 幂函数分析法
- 折线分析法
- 线性时变参量电路分析法
非线性电路主要可以应用在：
- 实现信号频谱的线性变换(频谱搬移)
- 实现信号频谱的非线性变换
- 实现变参量电路
参考资料
- 《通信电子线路》（第三版）：严国平，龙占超
- 老师课件
- 通信电子线路mooc