Introduction
与RNN、CNN等模型不同，Transformer模型中用到的attention机制无法捕捉输入顺序，这导致其无法区分不同位置的Token，因此我们需要额外引入位置信息到Transformer中，这也就引发了研究者们对位置编码的研究，具体而言，位置编码大体上可以分为以下几类：
- 绝对位置编码： 直接将位置信息以某种方式编码成向量，加入到输入中。
- 相对位置编码： 对Attention结构进行微调，使其有能力辨别不同位置的Token
- 其他位置编码： 包括相对位置编码和绝对位置编码的混合使用等其他不同寻常的位置编码
此外，对于位置编码而言，其长度外推性也是一个十分重要的考量，在此我们将单开一个章节讨论各种位置编码的长度外推性。
Absolute Position Embedding
从形式上来看，绝对位置编码是相对实现起来较为简单的方案，一般来说，绝对位置编码会被加入到输入中。即在输入的第\(k\)个向量\(x_k\)中加入位置向量\(p_k\)，即\(x_k' = x_k + p_k\)。具体而言，绝对位置编码还可以分为以下几个小类
训练式
最简单的方法是不进行特意设计位置编码，而是直接将位置编码可作为可训练参数，与模型其他参数一起，在训练过程中更新。这种方法因为其简单的实现方法往往应用较广，BERT,GPT等语言模型都是用这种方法。视觉里面的许多模型也使用这种方法，例如Mage, MAE , MAR等我们较为关注的掩码自回归模型等。
对于训练式位置编码，虽然其简单易实现，但是其最大的缺点是其没有外推性，即如果预训练最大长度为512时，那么在推理的时候，模型也就最多只能处理长度为512的序列。但也并非绝对，在苏神的博客层次分解位置编码，让BERT可以处理超长文本中，提出了通过使用层次分解位置编码，让BERT可以处理超长文本。其核心思路是通过层次分解，在已训练好的绝对位置编码向量上，通过线性插值的方式，得到新的位置编码向量。这样一来能实现在原来的参数基础上，能表示\(n^2\)的长度编码，且前n个位置编码与原编码相容。
三角式
三角式绝对位置编码，则是在Transformer原文《Attention is all you need》中提出的显式解，其公式表达为： \[\begin{cases} p_{k,2i} = sin(\frac{k}{10000^{2i/d}}) \\ p_{k,2i+1} = cos(\frac{k}{10000^{2i/d}}) \end{cases}\qquad(1)\]
其中\(d\)为位置向量的维度，\(k\)为位置索引，\(i\)为维度索引。
三角式位置编码的特点是拥有显式生成规律，其具有一定的外推性，另外得益于三角函数的性质，位置\(\alpha+\beta\)的向量可表示为位置为\(\alpha\)和\(\beta\)的向量的线性组合，这使得三角函数天生具有相对位置计算的性质。可惜的是这类绝对位置编码最近很少使用，待通过实验考证其原因。
递归式
在递归式绝对位置编码中，其往往实现为在输入之后衔接一层RNN，然后再接Transformer,那么其在结构上就有了通过RNN学习到位置信息的可能，比如从一个向量\(p_0\)开始，通过\(p_{k+1} = f(p_k)\)得到位置\(k+1\)的位置向量，在ICML2020的论文《Learning to Encode Position for Transformer with Continuous Dynamical Model》中，作者提出用微分方程建模位置编码，\(dp_t/d_t=h(p_t,t)\)，并使用神经网络来拟合\(h(p_t)\)，从而得到位置向量。此方法也被称为FLOATER。
Relative Position Embedding
与绝对位置编码不同的是，相对位置编码并没有完整的去建模每个输入的位置信息，而是在计算Attention的时候考虑了当前位置和被attention的位置的相对距离，对于相对位置编码来说，其实现上可能相较绝对位置编码更为复杂，但是其可解释性和灵活性更强。往往相对位置编码能取得比绝对位置编码更灵活的外推性能
经典式
相对位置编码起源于Google论文《Self-Attention with Relative Position Representations》，后面的各种相对位置编码变体基本上也是在此基础上的不同修改。
一般认为，相对位置编码是从绝对位置编码启发而来，考虑一般的带绝对位置编码的Attention: \[\begin{cases} q_i = (x_i + p_i)W_Q \\ k_j = (x_j + p_j)W_K \\ v_j = (x_j + p_j)W_V \\ a_{i,j} = softmax(q_i k_j^T) \\ o_i = \sum_{j} a_{i,j} v_j \end{cases}\qquad(2)\]
在此处，初步展开\(q_ik_j^T\)，有： \[q_ik_j^T = (x_i + p_i)W_Q(x_j + p_j)^TW_K^T = (x_iW_Q+p_iW_Q)(W_K^Tx_j^T+W_K^Tp_j^T)\qquad (3) \]
为了引入相对位置信息，Google将第一项位置去掉，第二项\(p_jW_K^T\)保留，并将其记为\(R_{i-j}\)，即： \[a_{i,j}=softmax(x_iW_Q(x_jW_K+R_{i,j}^K)^T)\qquad(4)\] 并将\(o_i\)表达式中的\(p_jW_v\)替换为\(R_{i,j}^V\)，即： \[o_i = \sum_{j} a_{i,j} (x_jW_V+R_{i,j}^V)\qquad(5)\]
替代的向量\(R_{i,j}^K\)和\(R_{i,j}^V\) 通常是只依赖与相对距离\(i-j\),并会进行截断以适应不同的距离 \[R_{i,j}^K = p_K[clip(i-j,p_{min},p_{max})]\\ R_{i,j}^V = p_V[clip(i-j,p_{min},p_{max})]\qquad(6)\]
这样就通过有限个位置编码实现了表达任意长度的相对位置(因为进行了截断操作)。
XLNET式
XLNET式源自Transformer-XL《Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context》，其源自于对上面的\(q_ik_j^T\)的完全展开： \[q_ik_j^T = x_iW_QW_K^T x_j^T+x_iW_QW_K^Tp_j^T+p_iW_QW_K^Tx_j^T+p_iW_QW_K^Tp_j^T\qquad(7)\]
Transformer-XL的做法是直接将上式的\(p_j\)替换为相对位置向量\(R_{i-j}\)，两个\(p_i\)则直接替换为两个可训练的向量\(u,v\): \[x_iW_QW_K^Tx_j^T+x_iW_QW_{K,R}^TR_{i-j}^T+uW_K^Tx_j^T+vW_{K,R}^TR_{i-j}^T\qquad(8)\]
此外，\(v_j\)上的位置偏置就直接去掉了，直接令\(o_i=\sum_ja_{i,j}x_jW_V\)，从此工作后，后面的相对位置编码工作都只加到Attention矩阵而不加到\(v_j\)上去了。
T5式
T5式相对位置编码源自于T5《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》，里面对展开式(7)进行了更详细的含义划分，其分别理解为"输入-输入"，"输入-位置"，"位置-输入"，"位置-位置"四项注意力组合，其认为输入信息和位置信息应该是独立的，那么"输入-位置"和"位置-输入"的注意力可以删掉 而其实位置-位置的注意力是一个只依赖于\((i,j)\)的标量，可以直接作为参数训练出来，即简化为 \[x_iW_QW_K^Tx_j^T=\beta_{i,j}\qquad(9)\]
也就是其只是在Attention矩阵的基础上加一个可训练的偏置项\(\beta_{i,j}\) 就实现了相对位置编码。
DeBERTa式
DeBERTa式相对位置编码源自于DeBERTa《DeBERTa: Decoding-enhanced BERT with Disentangled Attention》，其也是从展开式(7)出发，但是其丢弃的是第四项"位置-位置"注意力，保留第2、3项并且替换为相对位置编码 \[q_ik_j^T = x_iW_QW_K^Tx_j^T+x_iW_QW_K^TR_{i,j}^T+R_{j,i}W_QW_{K}^Tx_{j}^T\qquad(10)\]
Other Position Embedding
复数式
该想法来自论文《Encoding word order in complex embeddings 》。其使用复数域词向量编码词序，是第一个将复数的虚部域具体含义(词序)联系起来的工作。其推导出了复数域的词向量形式： \[f(j,pos)=[r_{j,1}e^{i(w_{j,1}pos+\theta_{j,1})},\dots,r_{j,2}e^{i(w_{j,2}pos+\theta_{j,2})},\dots,r_{j,D}e^{i(w_{j,D}pos+\theta_{j,D})}]\qquad(11)\\r_j:振幅,w_j:角频率，\theta_j：初相位\]
复数词向量的振幅\(r_j\)只与词\(w_j\)有关，对应token embedding。 角频率\(w_j\)可以表示词对位置的敏感程度，角频率越小对位置越不敏感，但其缺点在于因为需要维护振幅、角频率和初相位，参数量相当于三倍
RoPE
RoPE由苏神在《ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING》中提出，其将绝对位置编码和相对位置编码融为一体。简单来说其对attention里面的向量内积先用复数表示为: \[<q_m,k_n>=Re[q_mk_n^*]\qquad(12)\] 进一步将\(q_m,k_n\)分别乘以\(e^{im\theta},e^{in\theta}\)变为\(q_me^{im\theta},k_ne^{in\theta}\),然后放到内积变为: \[<q_me^{im\theta},k_ne^{in\theta}>=Re[q_mk_n^*e^{i(m-n)\theta}]\qquad(13)\] 上式就得出了内积只依赖于相对位置\(m-n\)的结论，巧妙地将绝对位置和相对位置结合到一起。 这样一来，我们得到了二维情况下用复数表示的RoPE: \[f(q,m)=R_f(q,m)e^{i\theta_f(q,m)}=||q||e^{i(\theta(q)+m\theta)}\qquad(14)\] 还可以将其写为矩阵形式： \[f(q,m)=\begin{pmatrix} cos m\theta & -sin m\theta \\ sin m\theta & cos m\theta \\ \end{pmatrix}\begin{pmatrix} q_0\\ q_1 \end{pmatrix}\qquad(15)\]
其优势是通过绝对位置编码的方式实现了相对位置编码，现在得到了广泛使用
Length Extrapolation
长度外推一般指的是不需要用长序列数据进行额外的训练，只用短序列语料对模型进行训练，就可以得到一个能够处理和预测长序列的模型。但是值得注意的是长度外推不能以牺牲远程依赖为代价，这样还不如直接截断文本进行生成。
在长度外推问题中，遇到的主要问题有以下两点： 1. 预测时用到了没有被训练过的位置编码 2. 预测时注意力机制所处理的tokens数量远超训练时的数量
事实上，对于相对位置编码的Transformer可以通过简单的Attention Mask一次性解决上述问题，并取得接近SOTA的效果。其具体操作时将预测时的attention变为局部attention, 每个token只看到训练长度个token 且此时的局部attention也不会比训练时使用更多的位置编码, 这样就一次性解决了上面的问题，且不用重新训练模型。
ALIBI
ALIBI是第一篇明确研究Transformer长度外推性的工作，其出自论文《Train Short, Test Long: Attention with Linear Biases Enables Input Length Extrapolation》。它主要是在Softmax之前，将attention的计算从\(q_m^Tk_n\)改为 \[q_m^Tk_n-\lambda|m-n|\qquad (16)\] ALIBI相较于上面用attention mask解决长度外推问题的基线模型，减去的非负矩阵更光滑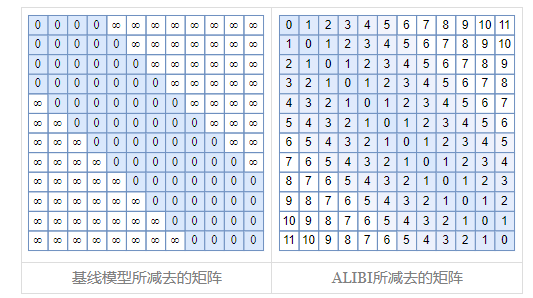 
但是从(16)中可以看出ALIBI是只能辨别相对距离远近，而无法正确识别位置信息的,因为\(|m-n|=|n-m|\)。其主要是在单项语言模型上效果较好，因为单项语言模型不加位置编码也能取到较好效果
KERPLE
KERPLE来自论文《KERPLE: Kernelized Relative Positional Embedding for Length Extrapolation》,是ALIBI的简单推广，引入了两个训练参数\(r_1,r_2\)来一般化式(16): \[\begin{cases} q_m^Tk_n-r_1|m-n|^{r_2},\qquad r_1>0,0<r_2\le2\\ q_m^Tk_n-r_1log(1+r_2|m-n|),\qquad r_1,r_2>0\\ \end{cases}\qquad(17)\]
其既完成了一般化又有可训练参数
Sandwich
Sandwich出自论文《Dissecting Transformer Length Extrapolation via the Lens of Receptive Field Analysis》，将式(16)替换为 \[q_m^Tk_n+\lambda p_m^Tp_n\qquad(18)\] 其中\(p_m,p_n\)是Sinusoidal 位置编码，\(\lambda>0\)是超参数
XPOS
XPOS出自论文A Length-Extrapolatable Transformer, 其是对RoPE的推广： \[RoPE:q_m\rightarrow R_mq_m, k_n\rightarrow R_nk_n\qquad XPOS: q_m\rightarrow R_mq_m\xi^m,k_n\rightarrow R_nk_n\xi^{-n}\qquad(19)\] 这样一来attention的计算变为 \[q_m^Tk_n=q_m^TR_{n-m}k_n\xi^{m-n}\qquad(20)\] 最后的结果只依赖于相对位置\(m-n\),但其指数部分是\(m-n\)而非绝对值，导致其总有一边是发散的
基于RoPE的长度外推
最近一年内，大部分的LLM的长度外推新工作都集中在研究基于RoPE的长度外推，其备受推崇的原因在于： 1. RoPE不带显式的远程衰减，这对于旨在Long Context的模型至关重要 2. RoPE是一种真正的位置编码，通过不同频率的三角函数有效区分长程短程，达到了类似层次位置编码的效果 3. RoPE直接作用于Q、K，不改变Attention形式，与Flash Attention更契合，更容易Scale Up
PI
PI(Positional Interpolation) 由Meta在论文《Extending Context Window of Large Language Models via Positional Interpolation》提出，其通过位置内插的方法将预测长文本的位置编码乘上放缩因子\(\frac{L_{train}}{L_{test}}\)缩放到训练长度内，但其缺点是会压缩临近Token的距离，扰乱局部分辨率，比如训练时长度为n，推理时长度为4n，做缩放时就会导致不同token之间的距离被压缩为原来的\(1/4\)，但其优势在于可以通过微调快速弥补此处的问题，适用于做模型初始化，然后再进一步微调得到长文本模型。
Leaky ReRoPE and ReRoPE
直接外推的问题是远处越界，位置内插的问题是局部失真，Leaky ReRoPE和ReRoPE通过先设定一个窗口大小\(w\),再将相对位置分为两部分，在窗口不改变相对位置实现"局部不失真"，在窗口外使用位置内插实现"远处不越界" 
如果将内插因子\(k\)取到无穷大，即可得到极简的ReRoPE，在窗口外的位置编码都变为\(w\),则其对任意长的序列都不会越界，但问题在于二者的实现稍微麻烦，因为二者的相对位置是分段线性的，所以朴素实现需要算两次Attention矩阵后再拼接
NTK-RoPE
NTK-RoPE的思路是将原本是\(\theta_i=10000^{-2i/d}\),现在改为了\(\theta_i=(10000k)^{-2i/d}\),\(k\)的取值是通过令\(i=d/2-1\)时的Scale正好等于内插Scale\(\frac{L_{train}}{L_{test}}\),得出方程 \[(10000k)^{-2i/d}|_{i=d/2-1}=\frac{L_{train}}{L_{test}}(10000)^{-2i/d}|_{i=d/2-1}\qquad(21)\] 求解得出 \[k=(\frac{L_{test}}{L_{train}})^{d/(d-2)}\qquad(22)\] 这样的设计基于作者对NTK的经验，判断高频\((i\rightarrow0)\)是学习相对距离的，不用改变，低频\((i\rightarrow d/2-1)\)是学习绝对距离的，所以要进行内插，其实际上只能让模型正常外推到\(L_{test}/2\)。因为从实际情况来看,只让最后一个\(i=d/2-1\)做完整内插，这种内插是不够充分的，于是作者推出了后续的YaRN。
YaRN
YaRN出自《 YaRN: Efficient Context Window Extension of Large Language Models》，是一种免训练长度外推方案，其只改变\(\theta_i\)的值，不改变Attention和RoPE形式，所以不会有额外的实现成本和推理成本，其可用公式表达为： \[\theta_i^{new}=[\gamma_i+(1-\gamma_i)\frac{L_{train}}{L_{test}}]\theta_i,\gamma_i=\begin{cases}
1,\qquad r_i>\tau\\
0,\qquad r_i<1\\
\frac{r_i-1}{\tau-1}.\qquad others
\end{cases}\qquad(23)\]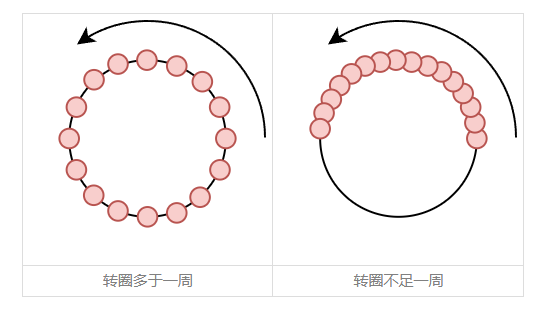 
YaRN认为较大的\(\theta_i\)意味着转速越快，周期越短，于是在\(m−n\)从0到\(L_{train}−1\)期间，它已经被转了很多圈，也就是说圆上的每一个点几乎都被训练过，因此这些\(\theta_i\)几乎不存在OOD问题；相反，对于较小的\(\theta_i\)，当\(m−n\)从\(0\)到\(L_{train}−1\)时它可能还没转完一圈，这种情况下被训练过的点顶多只是圆上的一条弧，如果测试时遇到更大的\(L_{test}\)，那么就超出了训练过的弧范围，从而有无法预估的表现，这时候就需要通过内插将它压缩到原本的弧内。
具体到上面的公式中的\(\theta_i\),可以算出周期为\(T_i=2\pi/\theta_i\),然后定义训练时所转的“圈数”为\(r_i=\frac{\theta_iL_{train}}{L_{test}}\),再设一个阈值\(\tau\)区分是否充分训练 二者间再使用线性插值过渡即可得出上述表达式
Dynamic Scaling
上面提到的免训练长度外推方法，都无法使得模型在训练长度\(L_{train}\)内的效果保持不变,一般的解决方法时随着训练长度变化动态调整各个外推方法的Scale因子，这就是Dynamic Scaling
以YaRN为例，里面与长度相关的缩放因子是\(s=\frac{L_{test}}{L_{train}}\), Dynamic Scaling将其换为动态的\(s(pos)=\frac{max(L_{train},pos+1)}{L_{train}}\), 其中pos是当前token的位置编号，这个改动意味着Dynamic Scaling试图为每个位置找到最小的、理论上对模型效果影响也最小的Scale因子。在此设计下，能避免在追求长度外推的过程中带来的训练长度内的效果下降。
Reference
- 【OpenLLM 009】大模型基础组件之位置编码-万字长文全面解读LLM中的位置编码与长度外推性（上）
- 【OpenLLM 010】大模型基础组件之位置编码-万字长文全面解读LLM中的位置编码与长度外推性（ 中）
- 苏剑林. (Mar. 23, 2021). 《Transformer升级之路：2、博采众长的旋转式位置编码 》[Blog post]. Retrieved from https://kexue.fm/archives/8265
- 苏剑林. (Feb. 03, 2021). 《让研究人员绞尽脑汁的Transformer位置编码 》[Blog post]. Retrieved from https://kexue.fm/archives/8130
- 苏剑林. (Jan. 26, 2024). 《Transformer升级之路：16、“复盘”长度外推技术 》[Blog post]. Retrieved from https://kexue.fm/archives/9948