前言

在学习邻接矩阵时，我们会发现一个有意思的现象，有时100*100的矩阵中只储存了10个数据，我们把这种矩阵称为稀疏矩阵，其适用于一个阶数较大的矩阵中的非零元素个数相对于矩阵元素的总个数很小，如果这种稀疏矩阵用邻接矩阵来储存，这是浪费了很多空间的，那么我们应当如何在保留其矩阵信息的前提下，用一个好的结构来节省空间的开支呢？

前言

最小生成树由一个经典的架电线的问题引出：在n个村庄间架电线，现在已经知道各村庄的相对距离，如果你是工程师，请问如何设计能使得总造价最小

解决思路

首先可以分析得到这显然是一个带权值的图，即网结构，我们的目标可以抽象为用n-1条边把一个连通图连接起来，并使得权值最小，这就是我们常说的最小生成树问题，最经典的两种算法是：prim算法和kruskcal算法，下文将一一介绍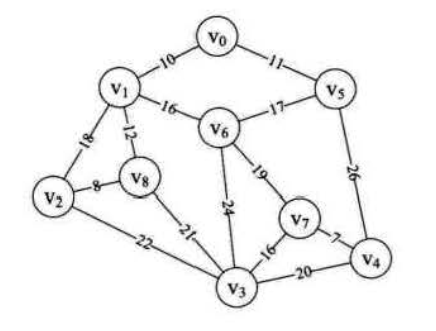

00 Gin框架简介

Gin是一个用Go语言编写的web框架，是一个拥有良好性能的API框架，其性能非常好，是GO世界里最流行的web框架，是一个简单易用的轻量级框架

次优查找树

前言

关于静态查找表中对特定关键字进行顺序查找，折半查找或者分块查找，都是在查找表中各关键词被查找概率相同的前提下进行的，然而在查找表中各关键字查找概率不同的情况下，折半查找的效果其实是不好的。在查找成功的情况下，描述查找过程的判定树其带权路径长度之和（用PH表示）最小时，查找性能最优，称该二叉树为静态最优查找树 其中: PH = 所有节点所在的层次数*每个节点对应的概率值 由于构造最优查找树花费的时间代价较高，而且有一种构造方式创建的判定树的查找性能同最优查找树只差1%-2%，称这种极度接近于最优查找树的二叉树为次优查找树

锦标赛排序

前言

这种排序方式的经典应用来自百度的一道面试题：给出一个长度是N的数组，现在要找出最小的两个元素，最少要多少次比较？