前言
本知识小结只针对华中科技大学电子信息与通信学院课程《通信原理》进行总结，不保证满足所有读者需求
6.1 数字基带信号及其频谱特性
6.1.1 数字基带信号
数字基带信号是指未经调制的数字信号，所占据的频谱从零频或很低频率开始的，数字基带传输系统是指不经载波调制而直接传输数字基带信号的系统，而下一章将讲述的数字带通传输系统则是包括调制和解调过程的传输系统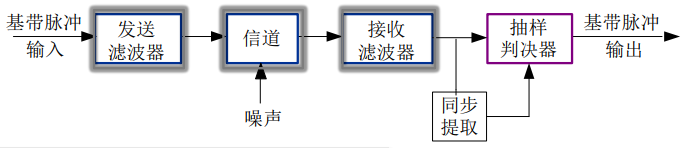 
在基带传输中的主要技术问题有以下几个：
- 基带传输系统通常存在隔直流电容或传输变压器，基带信号中的直流分量不能通过隔直流电容和变压器，克服措施--研究基带码的码型，寻求基本无直流分量的基带码
- 码元同步
- 码间串扰:前一码元波形拖尾干扰到后面若干个码元，克服措施--寻求合适的码元波形，使码间串扰不会引起接收判决错误；采用均衡技术，改善码元波形，减小码间串扰
具体来说，数字基带信号又可分为单/双极性波形，单/双归零码，差分波形
6.1.2 数字基带信号的频谱特性
数字基带信号可表示为\(s(t)=u(t)+v(t)\)，其功率密度可表示为 \[双边谱：P_s(f)=P_u(f)+P_v(f)=f_BP(1-P)|G_1(f)-G_2(f)|^2+\\\sum_{m=-\infty}^\infty|f_B[PG_1(mf_B)+(1-P)G_2(mf_B)]|^2\delta(f-mf_B)\] \[单边谱：P_s(f)=2f_BP(1-P)|G_1(f)-G_2(f)|^2+f_B^2|PG_1(0)+(1-P)G_2(0)|^2\delta(f)+\\2f_B^2\sum_{m=1}^\infty|[PG_1(mf_B)+(1-P)G_2(mf_B)]|^2\delta(f-mf_B)\] 由此可以得出以下结论：1. 二进制随机脉冲序列的功率谱包含连续谱和离散谱(可能包含)；连续谱总是存在的，谱的形状取决于\(g_1(t),g_2(t)\)频谱和出现概率P；离散谱是否存在也主要取决于以上三者
对于单极性NRZ和RZ矩形脉冲序列的功率谱，不加证明的给出结论(以下均默认P=0.5)
- 单极性NRZ频谱函数为\(P_s(f)=\frac{T_s}{4}Sa^2(\pi fT_s)+\frac{1}{4}\delta(f)\)
- 单极性RZ频谱函数为\(P_s(f)=\frac{T_s}{16}Sa^2(\frac{\pi fT_s}{2})+\frac{1}{16}\sum_{m=-\infty}^\infty Sa^2(\frac{m\pi}{2})\delta(f-mf_s)\)
- 双极性NRZ频谱函数为\(P_s(f)=T_BSa^2(\pi fT_B)\)
- 双极性RZ频谱函数为\(P_s(f)=\frac{T_B}{4}Sa^2(\frac{\pi}{2}fT_B)\)
6.2 基带传输的常用码型
选码原则：无直流分量，且低频分量小；定时信息丰富；高频分量小；不受信源统计特性的影响；有自检能力；编译码简单
常用的传输波形有AMI码,\(HDB_3\)码，双相码，CMI码，nBmB码，nBmT码
6.3 数字基带信号传输与码间串扰
6.3.1 系统组成与传输模型
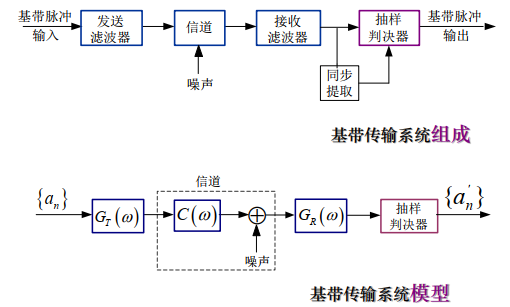
6.3.2 定量分析
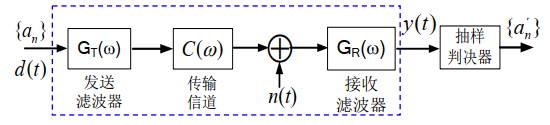基带传输总特性:\(H(w)=G_T(w)C(w)G_R(w)\),基带信号\(d(t)=\sum_{n=-\infty}^\infty a_n\delta(t-nT_B)\),接受滤波器输出信号为\(y(t)=d(t)*h(t)+n_R(t)=\sum_{n=-\infty}^\infty a_nh(t-nT_B)+n_R(t)\),设抽样时刻为\(t=kT_B+t_0\rightarrow a_kh(t_0)+\sum_{n\neq k}a_nh[(k-n)T_B+t_0]+n_R(kT_B+t_0)\),后两项为ISI值和噪声
6.4 无码间串扰的基带传输特性
6.4.2 五码间串扰的条件
消除码间串扰的基本思想是使得其他码元在当前码元的抽样判决点处值为0，由奈奎斯特准则知接收波形满足抽样值无失真传输的充要条件是码元仅在本码元的抽样时刻上有最大值，而其他所有码元在该时刻的串扰值均为0，其对应的时域条件为\[h(kT_B)=\begin{cases} 1,k=0\\ 0,else \end{cases}\] 频域条件\[\sum_iH(w+\frac{2\pi i}{T_B})=T_B,|w|\le\frac{\pi}{T_B}\]
6.4.3 H(w)的设计
理想低通特性 \[H(w)=\begin{cases} T_B,|w|\le\frac{\pi}{T_B}\\ 0,|w|>\frac{\pi}{T_B} \end{cases},h(t)=Sa(\frac{\pi}{T_B}t),B=\frac{1}{2T_B}=f_N,R_B=\frac{1}{T_B}=2f_N\]其中B又被称为奈奎斯特带宽：无失真传输码元周期为\(T_B\)的序列是所需的最小频带宽度，\(R_B\)又被称为奈奎斯特速率：在带宽为\(f_N\)的信道中无码间串扰的最高波特率,由此易得，无ISI基带系统的最高频带利用率\(\eta=R_B/B=2,\eta_b=R_b/B=2log_2M\),由上述公式可得以下重要结论：在无ISI的要求下，WHz宽的基带信道每秒最多只能传输2W个符号，无码间串扰要求\(\eta\le2 \quad or\quad\eta_b\le 2log_2M\),理想低通传输特性主要存在的问题是特性陡峭不易实现，工程上广泛使用的是余弦滚降特性
余弦滚降特性
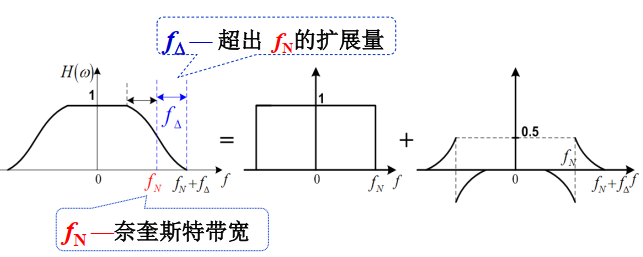引入滚降系数来描述滚降程度\(\alpha=\frac{f_\Delta}{f_N}(0\sim1)\),进而可推出\[B=f_N+f_\Delta=(1+\alpha)f_N,\eta=\frac{R_B}{B}=\frac{2}{1+\alpha},\eta_b=\frac{R_b}{B}=\frac{2log_2M}{1+\alpha}\] \(\alpha\)越大，\(h(t)\)的拖尾衰减越快,\(\alpha=0\)：理想低通特性，\(\alpha=1\)，升余弦频谱特性，其特点为特性易实现，代价是带宽增加，频率利用率降低
6.5 基带系统的抗噪声性能
本节主要讨论：在无码间串扰的条件下， 噪声对基带信号传输的影响， 即计算噪声引起的误码率，公式考试使会给出，主要掌握其结论 
上图表面，当比值\(A/\sigma_n\)一定时，双极性基带系统的误码率比单极性的低，抗噪声性能好；在等概条件下，双极性的最佳判决门限电平为0，与信号幅度无关，因而不随信道特性变化而变，故能保持最佳状态。而单极性的最佳判决门限电平为A/2，它易受信道特性变化的影响，从而导致误码率增大；双极性基带系统比单极性基带系统应用更为广泛
6.7 时域均衡
均衡是指对信号在传输过程的非线性失真进行校正，均衡器设计的两个基本途径分别是频域均衡和时域均衡，分别处理频域与时域，使系统无码间串扰，目的都是消除或减小码间串扰
具体来说，时域均衡的目标使调整各增益加权系数\(C_i\),使得除\(k=0\)外，y(t)在奈氏各取样点上的值均为0，消除了码间干扰,\[y_k=\sum_{i=-N}^Nc_ix_{k-i}=\begin{cases}
1,k=0\\
0,k\neq0
\end{cases}\] 均衡效果的评价一般采用峰值失真和均方失真\[D=\frac{1}{y_0}\sum_{k=-\infty,k\neq0}^\infty|y_k|,e^2=\frac{1}{y_0^2}\sum_{k=-\infty,k\neq0}^\infty y_k^2\],实际应用中常用迫零调整法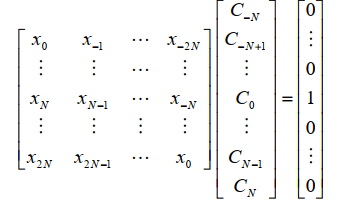 
参考资料
- 《通信原理》（第七版）：樊昌信，曹丽娜
- 老师课件